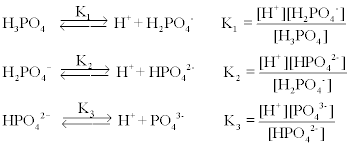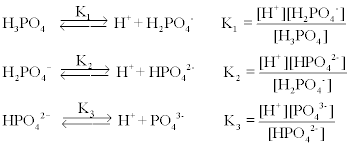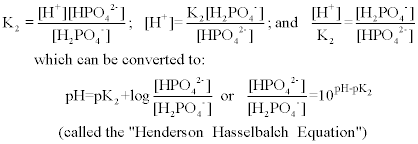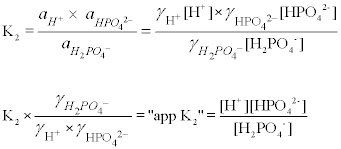Phosphate Buffers
Phosphoric acid is a triprotic acid which undergoes a stepwise dissociation as follows,
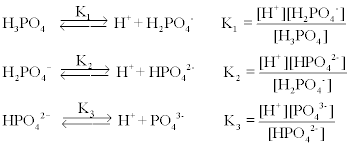
where K1 = 6.5 x 10-3 ; K2 = 6.2 x 10-8 ; and K3 = 3.6 x 10-13 . Each of these three equilibrium equations can be expressed mathematically in several different ways. Taking the equation for K2 as an example, each of the following is equivalent:
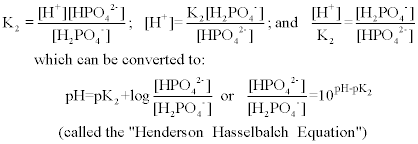
where pH = -log[H+ ], and pK2 = -logK2. The latter logarithmic expression (the "Henderson Hasselbalch Equation") is a convenient form to use in buffer calculations, particularly when the pH is within one unit above or one unit below the pK. (Where the ratio [HPO42-]/[H2PO4-] is between 0.10 and 10). Although all four species of phosphate are always present in solution, the two forms in the equation are the predominant ones near the pK and the others can usually be ignored in calculations. As one gets more than two units above or below the pK, however, other species become involved and the calculations get more complicated.
Phosphate acts best as a buffer in the reqions of pH near its three pK's: pK1 = 2.12, pK2 = 7.21; and pK3 = 12.44.
Complications and Caveats
When a weak acid dissociates, HA → H+ + A-, there is a separation of charges. The acid dissociates more easily in water than in a non-polar organic solvent because the water molecules are able to solvate the ions, effectively dampening the coulombic force of attraction between them. This dampening ability of water is reflected in its dielectric constant. A solution of ions in water is even more effective at dampening this attraction as the dissociated species can each become surrounded by a cloud of ions of opposite charge. Therefore an acid dissociates more easily in a salt solution than it does in water alone, so that
Ka values increase, and pKa values decrease, with increasing salt concentration!
But Ka and pKa are supposed to be constants! How can they change? The answer is that they refer to an "ideal solution", just as the ideal gas law refers to an ideal gas, and an ideal solution is one which is very dilute, essentially containing only water and devoid of other ions. Equilibrium equations therefore refer to "activities" of solutes, which differ from the actual concentrations by an "activity coefficient" (γ). In an ideal solution, the activity coefficient is one, but is different from 1 in a non-ideal solution. The HPO42- ion, for example, has an activity coefficient of about 0.5 in a 0.1 M solution, so its activity is given by γ[HPO42-], or (0.5 x 0.1) = 0.05. (Activities do not have units--they are ratios of concentrations to a "standard state" concentration, usually 1 M for solutes.)
The activity coefficients for each of the species in the equilibrium expression can be combined with the equilibrium constant to give a new "apparent" equilibrium constant in terms of molar concentrations. In the second dissociation of phosphate, for example, where a refers to activity:
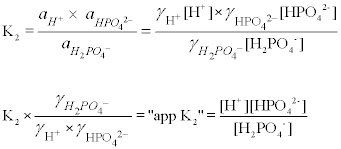
The activity coefficients of ionic species depend upon both its charge and the "ionic strength" of the medium, a relationship quantitatively described by the Debye-Hückle equation. The effect is greater for multivalent ions, hence polyprotic acids such as phosphate are affected more strongly than monoprotic acids. (Even the "apparent pK2" will vary slightly with pH because ionic strength increases as a proton dissociates). The pH meter is actually measuring -logaH+, rather than -log[H+]. The quantitative details of this relationship are beyond the scope of this introductory course.
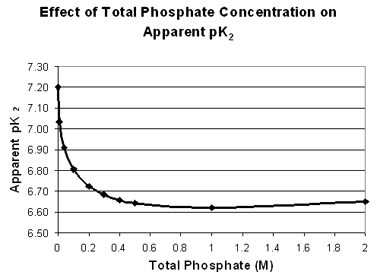
The main lesson for you with respect to this laboratory experiment is that one should use the appropriate pK2 value for calculations, depending on the total concentration of phosphate buffer involved, and recognize that even then there may be a slight deviation from expected pH values. Below is a table and a graph showing the effect of the phosphate concentration on the apparent pK2 value.
|
Total Phosphate
(M) | Apparent
pK2 |
| 0 | 7.20 |
| 0.01 | 7.03 |
| 0.04 | 6.91 |
| 0.10 | 6.81 |
| 0.20 | 6.73 |
| 0.30 | 6.68 | | 0.40 | 6.66 | | 0.50 | 6.64 | | 1.00 | 6.62 | | 2.00 | 6.65 |
|
| These values were calculated from data in A. A. Green, "The Preparation of Acetate and Phosphate Buffer Solutions of Known PH and Ionic Strength", J. Am. Chem. Soc. 55, 2331, (1933). as the average pK2 from the Henderson Hasselbalch equation over the pH range from 5.9 to 7.7. |