As was mentioned previously, one of the more important aspects of quantitative data is the ability to use it for comparison. This ability however is highly dependent on the units in which the data is expressed. In chemistry the scientists have come to agree upon a set of common units called the System de International (SI) base units that we all agreed to use when communicating our research findings. The table presented here lists all of the common SI base units. You should definitely familiarize yourself with the units, their symbols and what measurement type they represent.
| Base quantity | Name | Symbol |
| Length | meter | m |
| Mass | kilogram | kg |
| Time | second | s |
| Electric Current | ampere | A |
| Thermodynamic Temperature | kelvin | K |
| Amount of Substance | mole | mol |
| Luminous Intensity | candela | cd |
Three of the most commonly used units are those for length, mass and time. While the meter should be quite familiar to you, as meter sticks are slowly becoming as common as yard sticks in this country, the kilogram is probably not an amount or mass that you can picture readily in your head like you could a pound. There are in fact 2.2 lbs in a kilogram if that will help you picture it better. The reason the kilogram is used for the unit of mass is because the gram is such a small amount. I would much rather weigh 59 kg than 59,000g. As for time, although you might think the minute a better unit, the reality is that most chemical reactions happen very quickly and a minute is too large a unit to be very handy for expressing the time scale of these reactions.
| Definitions of SI Base Units | ||
| Unit of Length | Meter (m) | The meter is the length of the path travelled by light in vacuum during a time interval of 1/299,792,458 of a second. |
| Unit of Mass | kilogram (kg) | The kilogram is the unit of mass; it is equal to the mass of the international prototype of the kilogram. |
| Unit of Time | Second (s) | The second is the duration of 9,192, 631, 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom. |
The base units for Electric Current and temperature are the Ampere and the Kelvin, respectively. While we won’t use the unit for electric current often, it is good to know the basis for the unit. The Ampere is that constant current which travels at a rate of 1 coulomb per second. A Coulomb is in turn defined as 1 Ampere per second. Generally speaking both units stand for a package of electrical current that has a force equal to that of 2 x 107 newtons per meter of length.
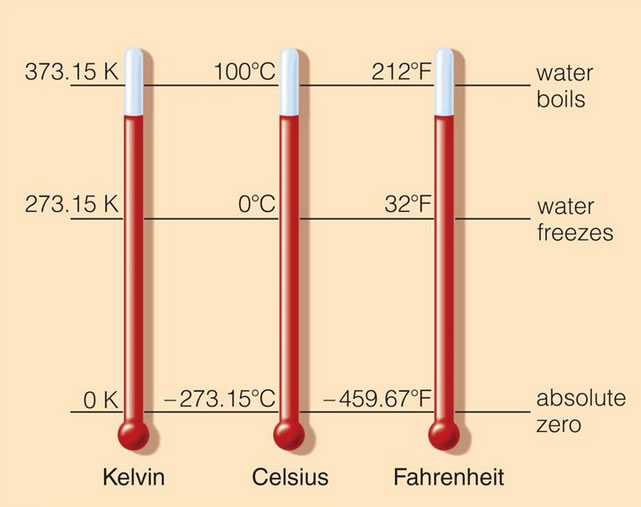
The kelvin (K) is the base unit for temperature. Kelvin is called the absolute temperature scale because it does not use degrees. The kelvin measurement intervals are equal to those of the Celsius degree scale. On the kelvin scale, absolute zero is 0 K and the triple point of water has the value of approximately -273.15 degrees Celsius. Therefore to convert from degrees Celsius to kelvin, you simply add 273.15 to the Celsius temperature. The Fahrenheit degree scale is not equivalent to the kelvin scale so further calculations must be completed to convert between those two temperature scales.
| Definitions of SI Base Units | ||
| Unit of Electric Current | Coulomb / Ampere (Amp) | The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 meter apart in vacuum, would produce between these conductors a force equal to 2 x 10-7 newton per meter of length. |
| Unit of Thermodynamic Temperature | Kelvin (K) | The kelvin, unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water. |
The last two SI base units we will discuss are those for the amount of a substance, the mole and the unit for luminous intensity ( a fancy way of saying how bright a light might be) called the Candela (I always think of candle light to help me remember this one).
The mole is a very important unit in chemistry and one we will be using in the near future A LOT. The official definition of the mole is that it is an amount of entities equal to the number of atoms in 0.012 grams of Carbon 12. While I know that does not make much sense right now, the important thing to know is that the value of the mole is 6.022 x 1023entities. So much in the same way you would say a dozen donuts and know that meant 12 donuts. If you say a mole of donuts, that means you have 6.022 x 1023 donuts and a very bad stomach ache. We will further define the mole in a later lecture and show how it is used in chemical calculations.
Two Moles Per Liter
(Chemistry Humor)
The candela is simply a measured unit of how bright/strong the light being produced by a source may be. It is equal to 1/683 of a watt which is a unit of power so long as it is measured in one direction. We will not use this unit much in this course but you should note that there may be times in an investigation where knowing the amount of light present and being able to quantify that amount of light would be valuable to a case. Think about eye-witness testimony. If the light present can be shown as too low for visibility, the eye-witness's statement could be thrown out.
| Definitions of SI Base Units | ||
| Unit of Amount of Substance | Mole (mol) | 1. The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12; its symbol is "mol." 2. When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles. |
| Unit of Luminous Intensity | Candela (cd) | The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 x 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian. |
Obviously units cannot be all that is allowed to describe the massive quantities and types of data collected by scientists and in fact there are many more units that can be used. These units, called "derived units" are called thus because they are created through the combination of the seven base units. This is what makes them "OK" for use in scientific communications. So long as your measurements start with the use of the SI base units, any manipulation or derivation that follows is allowed. Several of the more common derived units are shown in the table along with their derivation from the base units they use.
SI Derived Units
Other quantities, called derived quantities, are defined in terms of the seven base quantities via a system of quantity equations.
The SI derived units for these derived quantities are obtained from these equations and the seven SI base units. Examples of such SI derived units are given in the table below:
| Examples of SI Derived Units | ||
| SI Derived Unit | ||
| Derived Quantity | Name | Symbol |
| area | square meter | m2 |
| volume | cubic meter | m3 |
| speed, velocity | meter per second | m/s |
| acceleration | meter per second squared | m/s2 |
| wave number | reciprocal meter | m-1 |
| mass density | kilogram per cubic meter | kg/m3 |
| specific volume | cubic meter per kilogram | m3/kg |
| current density | ampere per square meter | A/m2 |
| magnetic field strength | ampere per meter | A/m |
| amount-of-substance concentration | mole per cubic meter | mol/m3 |
| luminance | candela per square meter | cd/m2 |
| mass fraction | kilogram per kilogram, which may be represented by the number 1 | kg/kg = 1 |
Temperature
Since temperature is very important in forensics, often determining time of death or recent activity of a motor etc. We need to discuss more about the temperature scales that are commonly used since thermometers and thermocouples almost never read out in kelvin units.
There are three temperature scales that are in common use in science and industry. Two of those scales are SI metric:
The degree Celsius (°C) scale was devised by dividing the range of temperature between the freezing (0°) and boiling (100°)temperatures of pure water at standard atmospheric conditions (sea level pressure) into 100 equal parts. Temperatures on this scale were at one time known as degrees centigrade, however it is no longer correct to use that terminology.
The kelvin (K) temperature scale is an extension of the degree Celsius scale down to absolute zero, a hypothetical temperature characterized by a complete absence of heat energy. Temperatures on this scale are called kelvins, NOT degrees kelvin, kelvin is not capitalized, and the symbol (capital K) stands alone with no degree symbol. [The official name was changed to "kelvin" and symbol "K" by the 13th General Conference on Weights and Measures (CGPM) in 1967.]
The degree Fahrenheit (°F) non-metric temperature scale was devised and evolved over time so that the freezing (32°) and boiling (212°) temperatures of water are whole numbers, but not round numbers as in the Celsius temperature scale.
The Fahrenheit temperature scale is "antiquated, clumsy, and still in use in only one industrialized nation in the world today - the United States."Walter A. Lyons, PhD
The Handy Weather Answer Book, page 41.
The Fahrenheit temperature scale is "plain silly and it's cultural value [is] slim."Neville Holmes
"The Numerical Dysfunction", Mathematical Intelligencer, 22(1), 2000-winter, page 8.
Temperature Conversions
The need to convert between these scales is obvious as you may often measure temperatures in Celsius or Fahrenheit scales but should report the temperatures in Kelvin for communication or publication.
The conversion from Kelvin to Celsius and back again are shown. The simple addition or subtraction of the value 273.15 will convert back and forth between the scales. This is possible because one degree Celsius is equal to 1 kelvin.
Temperature conversions between the Celsius and kelvin temperature scales:
$$ \text{Kelvin / degree Celsius conversions (exact):} \\ K = ^\circ C + 273.15 \\ ^\circ C = K - 273.15 $$
This simple conversion is not possible between the Fahrenheit scale and kelvin. The process is normally to take the Fahrenheit temperature and first convert it to Celsius and then to further change it to kelvin. The equations needed to convert from Fahrenheit to Celsius and vice versa are shown. Note the importance of the parenthesis in these equations. You must always complete the calculations on the inside of the parenthesis first and then solve the rest of the problem.
Temperature conversions between the Celsius and Fahrenheit temperature scales:
$$ \text{Degree Fahrenheit / Degree Celsius conversions (exact):} \\ ^\circ F = ( ^\circ C \times 1.8) + 32. \\ ^\circ C = ( ^\circ F - 32.) / 1.8 $$
Gary, can we set these examples up as a reveal so they can try the calculation first and then hit a box/button that gives the explanation and calculation below?
Let's practice an example problem. Normal body temperature is 98.6°F. What is this value on the Celsius scale?
Step by Step:
- First set up the equation Celsius is equal to Fahrenheit minus 32 degrees divided by 1.8.
- Input 98.6 for the Fahrenheit temperature, then subtract the 32 degrees from it.
- Divide the resulting 66.6 by 1.8.
This yields a temperature of 37 degrees Celsius. Now before we continue we should always look at the answer and ask ourselves if the value we just calculate makes sense. Because the Fahrenheit scale is much longer than the Celsius scale (32 degrees to 212 degrees rather than 0 degrees to 100 degrees) we should expect the value in Celsius to considerably lower than the value in Fahrenheit. Therefore our value of 37 degrees makes reasonable sense.
Example 1Worked Out:
Normal body temperature is 98.6°F. What is this value on the celsius scale?
\begin{align} C & = (F - 32) / 1.8 \\ C & = (98.6 - 32) / 1.8 \\ C & = 66.6 / 1.8 \\ C & = 37 \\ 98.6 ^\circ \text{ Fahrenheit } & = 37 ^\circ \text{ Celsius} \end{align}
Let's try a second example. The boiling point of water is 100° Celsius. What is this value on the kelvin and Fahrenheit scales?
Step by Step:
- Add 273.15 to the Celsius value given. The answer in kelvin is 373.15 K.
- Multiply the 100 degrees Celsius that was given by 1.8.
- Add the resulting 180 degrees to 32 degrees
This yields a Fahrenheit boiling point of 212 degrees. Again, we should double check to see if this makes sense and based on the same reasoning as before it does appear to be a reasonable value. Plus it was the given boiling point of water a few paragraphs back.
Example 2 Worked Out:
The boiling point of water is 100° Celsius. What is this value on the kelvin and Fahrenheit scales?
\begin{align} 100 ^\circ C + 273.15 & = 373.15 K \\ F & = (1.8 \times C) + 32 \\ F & = (1.8 \times 100) + 32 \\ F & = 180 + 32 \\ F & = 212 \end{align}
Mass
Now let's spend some more time with another of the most commonly measured values: mass. As we stated previously mass and weight are only interchangeable here on Earth. Mass actually measures the amount of the substance present while weight describes the effect of gravity on that mass. When we want to measure the mass of an object we use a balance. A balance sets the mass of the object in relation to the known amount of another object. If you change the location of measurement for a mass there is no difference because it is based on this comparison to an amount of matter but since the weight is dependent on gravity, the change in location can change its value. Remember the moon and Venus.
How are weight and mass different? To understand the differences we need to compare a few points:
- Mass is a measurement of the amount of matter something contains, while Weight is the measurement of the pull of gravity on an object.
- Mass is measured by using a balance comparing a known amount of matter to an unknown amount of matter. Weight is measured on a scale.
- The Mass of an object doesn't change when an object's location changes. Weight, on the other hand does change with location.
The most commonly used unit of mass in the metric system is the gram. Other units of mass and their equivalents in grams are as follows:
- 1 milligram = 1 mg = 0.001 gram
- 1 centigram = 1 cg = 0.01 gram
- 1 decigram = 1 dg = 0.1 gram
- 1 kilogram = 1 kg = 1000 grams
The metric prefixes milli, centi, and deci are used to describe amounts in 1/1000th, 1/100th, 1/10th of a gram respectively. The kilogram is 1000 grams and thus is used to describe larger masses. Most balances are set up to read in units of grams but may be capable of measuring masses as small as 0.1 milligrams or 0.0001 grams. It is important to know the metric prefixes and the values they represent.
Length
The third unit of measure that we use quite often is that for length. The SI base unit is the meter and as with the gram, the metric prefixes allow us to express measurements in a number of different sizes from the millimeter (1/1000 of a meter) to the kilometer (1000 meters). Additional measures not introduced before are those metric prefixes for 10 and 100, deka and hector. But the unifying feature of all these prefixes is that they are based on factors of 10.
Length is a measurement of distance or dimension.
The two main systems to measure length are the metric and the English system.
Metric System Prefixes:
| Prefix | kilo | hecto | deka | meter | deci | centi | milli |
| Abbreviation | k | h | dk | m | d | c | m |
| Example | kilometer | hectometer | dekameter | meter | decimeter | centimeter | millimeter |
| Multiplier | 1,000 | 100 | 10 | 1 | 0.1 | 0.01 | 0.001 |
If we need to express large or small values, we can use the metric prefixes to make the numbers more manageable. For instance, take the number 20,000 meters and using a metric prefix convert it into a simpler number to work with. Since there is 1000 meters in a kilometer if we divide 20,000 by 1000 we can express this number in kilometers. What about 0.0035 grams? How would you restate this using a metric prefix? Well, a milligram is 1/1000 of a gram. If we multiply 0.0035 grams by 1000 we can then express the 0.0035 grams as 3.5 grams. The metric prefixes just make it easier to express and work with very large and small numbers. So long as you know the value they represent converting between the values just requires simple algebra.
Example
What metric prefix would make the number 20,000 meters more manageable?
$$ 20,000 \text{meters} \times 1\text{km}/1000\text{m} = 20\text{km (kilometers)} $$
What about 0.0035 grams? How would you restate this using a metric prefix?
$$ 0.0035 \text{grams} \times 1000\text{mg}/ 1\text{g} = 3.5\text{mg (milligrams)} $$
What if we ask the question: "How many milligrams are in 2.56 kilograms?" The two prefixes kilo and milli are used in this question and both have a relationship to each other passing through the main unit of grams. Kilo means there are 1000 or 103 grams and there are 1000 or 103 milligrams in a gram, so if we place these values into a form to convert from kg to mg we see that the answer is 2.56 x 106 mg.
Let's try it again. How many kilometers would you find in 123 dekameters? Again, we need to gather up our prefix meanings. Kilo means there are 1000 meters, and there are 10 meters in a dekameter. Putting these factors together in a manner that will allow the values to be converted we determine that there are 1.23 km in 123 dkm.
Two things to note about our calculations: 1) if done properly all of the units that we do not want to use should cancel out and 2) the answers again should be checked to make sure they make sense. In our first question we note that while a kilogram is a large unit, millograms are small units so there should be a great many milligrams in a kilogram which is what we found. In the other example the values of our prefixes vary by a factor of a 100 (10 goes into 1000 one hundred times) so the value of the number of dekameters in a kilometer should vary by a factor of 100 which it does, 123 divided by 100 is 1.23.
Example: Gary, Let's make these pop-up answers as well so the student can try it on their own before seeing the answer.
How many milligrams are in 2.56 kilograms?
$$ 2.56 \text{kg} \times (1000\text{g}/1\text{kg}) \times (1000\text{mg}/1\text{g}) = 2.56 \times 10^6\text{mg} $$
How many kilometers would you find in 123 dekameters?
$$ 123 \text{dkm} \times (10\text{m}/1\text{dkm}) \times 1 (\text{km}/1000\text{m}) = 1.23 \text{km} $$