
The content that follows is the substance of lecture 18. In this lecture we cover the Gas Laws: Charles',Boyle's,Avagadro's and Gay Lussacs as well as the Ideal and Combined Gas Laws.
There are 4 general laws that relate the 4 basic characteristic properties of gases to each other. Each law is titled by its discoverer. While it is important to understand the relationships covered by each law, knowing the originator is not as important and will be rendered redundant once the combined gas law is introduced. So concentrate on understanding the relationships rather than memorizing the names.
Charles' Law- gives the relationship between volume and temperature if the pressure and the amount of gas are held constant:
1) If the Kelvin temperature of a gas is increased, the volume of the gas increases. (P, n Constant)
2) If the Kelvin temperature of a gas is decreased, the volume of the gas decreases. (P, n Constant)
This means that the volume of a gas is directly proportional to its Kelvin temperature. Think of it this way, if you increase the volume of a gas and must keep the pressure constant the only way to achieve this is for the temperature of the gas to increase as well.

Calculations using Charles' Law involve the change in either temperature (T2) or volume (V2) from a known starting amount of each (V1 and T1):

Boyle's Law - states that the volume of a given amount of gas held at constant temperature varies inversely with the applied pressure when the temperature and mass are constant.
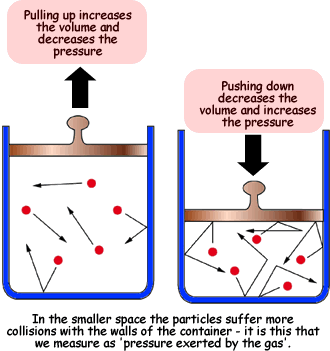
The reduction in the volume of the gas means that the molecules are striking the walls more often increasing the pressure, and conversely if the volume increases the distance the molecules must travel to strike the walls increases and they hit the walls less often thus decreasing the pressure.
Like Charles' Law, Boyle's Law can be used to determine the current pressure or volume of a gas so long as the initial states and one of the changes is known:

Avagadro's Law- Gives the relationship between volume and amount of gas in moles when pressure and temperature are held constant.
If the amount of gas in a container is increased, the volume increases. If the amount of gas in a container is decreased, the volume decreases. This is assuming of course that the container has expandible walls.
The relationship is again directly proportional so the equation for calculations is
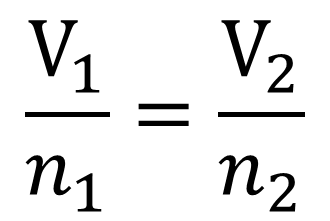
Gay Lussac's Law - states that the pressure of a given amount of gas held at constant volume is directly proportional to the Kelvin temperature.
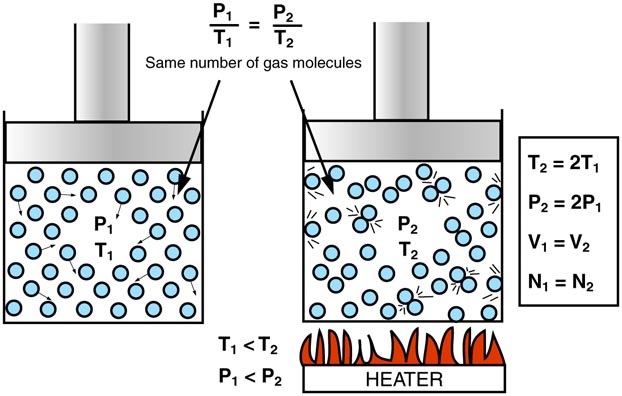
If you heat a gas you give the molecules more energy so they move faster. This means more impacts on the walls of the container and an increase in the pressure. Conversely if you cool the molecules down they will slow and the pressure will be decreased.
To calculate a change in pressure or temperature using Gay Lussac's Law the equation looks like this:

To play around a bit with the relationships, try this simulation.
A combination of the laws presented above generates the Ideal Gas Law:
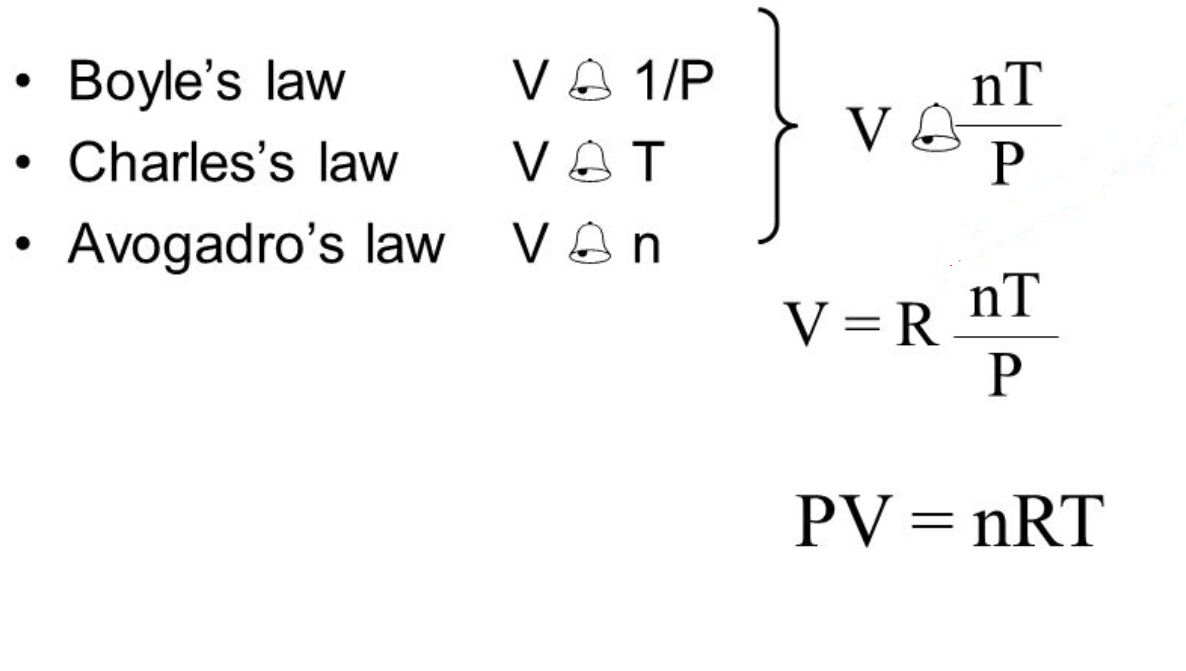
The addition of a proportionality constant called the Ideal or Universal Gas Constant (R) completes the equation.
As you can see there are a multitude of units possible for the constant. The only constant about the constant is that the temperature scale in all is KELVIN.
When using the Ideal Gas Law to calculate any property of a gas, you must match the units to the gas constant you choose to use and you always must place your temperature into Kelvin.
To use the equation, you simply need to be able to identify what is missing from the question and rearrange the equation to solve for it.
A typical question would be given as 6.2 liters of an ideal gas are contained at 3.0 atm and 37 °C. How many of this moles of the gas are present?
Because the units of the gas constant are given using atmospheres, moles, and Kelvin, it's important to make sure you convert values given in other temperature or pressure scales. For this problem, convert °C temperature to K using the equation:
T = °C + 273
T = 37 °C + 273
T = 310 K
Now, you can plug in the values. Solve for the number of moles
n = PV / RT
n = ( 3.0 atm x 6.2 L ) / ( 0.08206 L atm /mol K x 310 K)
n = 0.75 mol
Here are some practice problems using the Ideal Gas Law: Practice
I said above that memorizing all of the equations for each of the individual gas laws would become irrelevant after the introduction of the laws that followed. The law I was referring to is the Combined Gas Law:

The combined gas law allows you to derive any of the relationships needed by combining all of the changeable peices in the ideal gas law: namely pressure, temperature and volume. R and the number of moles do not appear in the equation as they are generally constant and therefore cancel since they appear in equal amounts on both sides of the equation.

As you can see above, the equation can be solved for any of the parameters in it. But more importantly, you can eliminate from the equation anything that will remain constant.
For Example, If a question said that a system at 1atm and a volume of 2 liters, underwent a change to 3.5 liters, calculate the new pressure, you could simply eliminate temperature from the equation and yield:

P2 = P1V1/V2 = (1atm)(2L)/3.5L) = 0.6 atm
Since the question never mentions a temperature we can assume it remains a constant and will therefore cancel in the calculation. You should also think about the answer you get in terms of what you know about the gases and how they act. We increased the volume so the pressure should go down. Checking our answer, this appears to be correct since the pressure went from 1atm to 0.6atm.
So the only equation you really need to know is the combined gas law in order to calculate changes in a gas' properties.
Here are some practice problems with solutions: Practice
Here are some problems for the other gas laws that you can derive from the combined gas law: Practice and KEY