Background

During the past century scientists like Sir J.J. Thomson, Ernest Rutherford, and Niels Bohr studied atomic structure. These studies concluded with the development of several different models, each attempting to further describe the internal structure of the atom. The Bohr model of the atom is especially easy to visualize. Chapter 5 of your textbook describes the development of these models and also describes the calculation of energy and wavelengths.

The Hydrogen Atom

The structure of the hydrogen atom is very simple: one proton and one electron, a phenomenon known for some time before Bohr. It was also known that the electron is negatively charged while the proton is positively charged. This created some intellectual difficulty for scientists: they did not understand why the electron doesn’t spiral into the proton—since negative charges are attracted to positive charges—and completely destroy the atom. But, since hydrogen is a stable atom, this attraction was obviously not the only rule that governed the behavior of the atom.           

Understanding why atoms are stable was a very important problem. Even the most advanced physics of the time, Maxwell’s Theory of Electromagnetism, predicted the instability of atoms. There was clearly a very fundamental flaw in their understanding of the universe.

Max Planck, Niels Bohr, and Energy

Prior to Niels Bohr’s model of the hydrogen atom, Max Planck had postulated that light was composed of photons that carried quanta, discrete packets of energy. Utilizing this notion, Bohr theorized that since there were well defined states in which atoms could exist, then photons with just the right energy could cause transitions between these states. In fact, the reason that the electron did not spiral into the proton was that the atom was actually in one of these stable states. Therefore, Bohr's theory also stated that the electrons were quantized in energy levels.

Quantization
 
The idea of quantization is often difficult to accept. In the macroscopic world, things are continuous; they can take on any value. For example, a car can travel 17 mph, 18 mph, or 17.5 mph; it is not restricted to only integer values. The speed is perceived on such a large scale that we cannot tell it is quantized, so it appears to be continuous. However, when examined more closely, this continuity no longer holds. The speed of the car is in fact quantized, but since the difference between two adjacent levels is so small, quantization cannot be observed.

Quantization actually means that only specific values are allowed. For example, consider a set of steps and a ramp. Since potential energy is a function of height, the potential energy is quantized for the steps. An object can rest only on one step or another; it cannot be between steps for a considerable amount of time. Thus, the potential energy increases only in increments of the height of the step. On the other hand, the ramp is not bound by such restrictions. For the ramp, the potential energy is continuous.  

The Predictions and Mathematics
In order to fully understand Bohr's predictions, some math is involved. Bohr's model predicted that the energy of a hydrogen atom was quantized, and that the energy of the atom was dependent on the principal quantum number (n), which is always an integer. The exact dependence of the energy on this value is complicated to derive, but it turns out that the energy, often abbreviated En, is given by the equation shown below where β is a constant based on Planck’s constant, the mass of the electron, and the charge of the electron. The value of b is ~2.18 x 10-18 Joules.

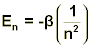
Note that the energy is negative.  If En is thought of as a measure of the energy of attraction between the electron and proton, we can see that the larger the value of n, the less negative the value of En. This means that there is less attraction between the electron and the proton, so the distance between them increases. When n is very large, the value of En approaches zero and there is no attraction between the electron and the proton. Therefore, the electron is free to go wherever it wants—it is no longer bound to the proton.

It should also be noted that the smallest value of n is one; thus the lowest energy state for hydrogen atoms is the value of β, not zero as one might expect. In fact, the only time the energy of the electron is zero is when it approaches an infinite distance from the nucleus.

Rydberg Equation

By itself, the equation given above is not very useful. Because there is no energy parameter used to measure the absolute energy, only energy differences can be measured. Consider two possible states of the hydrogen atom that has quantum numbers nI and nF. (Note: nI and nF stand for n initial and n final, respectively. These are the initial energy level from which the electron transfers and the final energy level where it ends up.)  If we consider a transition from the nI level to the nF level, the change in energy (ΔELevel) will be:

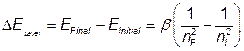
The change in energy values calculated using  this equation is positive if absorption is occurring (i.e. when the electron moves from a lower energy state to a higher energy state) and negative if emission is occurring (ie.when the electron is moving from a higher energy state to a lower energy state.) This energy is equal to the energy of the photon that either was absorbed or released by the atom. The energy of a photon with a frequency n is simply the value of that frequency multiplied by Planck’s constant (h), which is 6.626 x 10-34 J-sec.

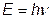
Furthermore, since the frequency is equal to the speed of light (c), 3.00 x 108 m/sec, divided by the wavelength (λ) of the photon in meters:
 

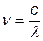
we can solve for the specific wavelength of light that is associated with a given transition. This is known as the Rydberg equation and is shown below.
 

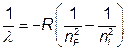
In this equation, R is known as the Rydberg Constant (1.10 x 10-2 nm-1) and takes into account Planck’s constant, as well as the speed of light, and has units that are more practical for calculating wavelengths. Although calculations may result in negative values of wavelength, only positive values are reported.
             

This Week’s Adventure
The Rydberg equation predicts a measurable value, the wavelength of light emitted by a transition between two states. For this experiment, nF will always be 2, the value corresponding to the visible spectrum. Therefore, by substituting values for nI that correspond to the visible spectrum of hydrogen, we can predict the wavelengths we should observe.

In this experiment, we will excite helium and hydrogen atoms by subjecting them to an electrical potential in a lamp. We will also excite a variety of cations by heating them in a flame. Each of these lamps or flames will be marked as unknowns. It will be your job to use your knowledge of their known wavelengths to identify them.

The Spectroscope
 
The spectroscope used in the experiment has a diffraction grating as its central component. A diffraction grating ‘bends’ light much like a prism. The angle at which the light is ‘bent’ depends upon the wavelength of light entering the grating.
Before we can start accurately measuring an unknown spectrum, we must first calibrate the spectroscope. You will use the known spectrum of helium, given in the table below, to calibrate your spectroscope. Once we plot the measured values of the helium lines against the known values, we can use that graph to determine the actual wavelengths of the unknown lamps and flames provided.