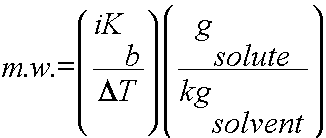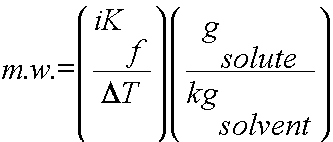
Colligative properties of solutions are properties that depend upon the concentration of solute molecules or ions, but not upon the identity of the solute. Colligative properties include vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure.

Lowering the Vapor Pressure:

Let's first remind ourselves about what vapor pressure is and what affects it chemically and physically. In a closed container, a liquid will evaporate until an equal amount of molecules are returning to the liquid state as there are escaping into the gas phase. The pressure of the vapor phase above the liquid at this point is called the equilibrium vapor pressure. This vapor pressure is dependent on a number of factors, including the temperature of the system (kinetic energy is required to help the molecules escape into the gas phase), the pressure of the system (high pressure can keep the gas contained in the liquid e.g. a bottle of coke), and also the intermolecular forces of the liquid itself (stronger bonds will require more kinetic energy to break slowing the evaporation process, lowering the overall vapor pressure of the system).

What happens to the system if we add a solute to the solvent in question? Well, in the simplest terms, since some of the solute molecules will take up spaces at the surface of the liquid, this will limit the number of solvent molecules at the surface. Since only solvent molecules located at the surface can escape (evaporate), the sheer presence of the solute lowers the number of solvent molecules coming and going and therefore lowers the equilibrium vapor pressure. In order to figure out how much the solute has affected the vapor pressure, we need to approximate how many fewer molecules are able to reach the surface of the liquid, correct? A good approximation of how many molecules there are of solvent versus solute is the mole fraction, X_solvent. If we simply multiply the new mole fraction of solvent by the standard vapor pressure (P^o_solvent) of the pure solvent, this will give us a good approximation of the new vapor pressure of the solvent. The equation would look like P_solvent = X_solvent P^o_solvent. This equation is called Raoult's Law. Note that the pressure you obtain from this equation is the new equilibrium vapor pressure of the system with the solute included. If you want to know how much change has taken place, you will need to look at the difference between the new P_solvent and the original P^o_solvent of the pure solvent (in other words subtract one from the other) DP = P_solvent - P^o_solvent = change in the vapor pressure of the system. For almost all non-volatile solvents, this change will be a negative value.

Limitations on Raoult's Law:

Raoult's law only works for low concentration solutions. Why? Well, in order for our approximation to work, the interactions between the solute and solvent molecules must be nearly identical. If the interactions are stronger, then the heat of vaporization of the solvent will change and thus our whole approximation falls apart. Since we know that intermolecular forces vary greatly between molecules, the affect of those forces must be kept at a minimum by keeping the solute concentration real low. You can think of it as having one stinky guy at a party in a room of 1000 people, there is a very good chance that you won't have to smell him, but if there were 100 stinky guys in the room, it would ruin the whole party, right?

Another consideration is the type of solute. If the solute is an ionic species (a salt) then it is most likely going to split up into its component ions when it hits the solvent (normally water). If this is the case, we need to consider each particle that forms. For instance, if you added 0.25 moles of NaCl to a solution, you would actually be adding 0.25 moles of Na⁺ and 0.25 moles of Cl^- for an overall colligative affect of 0.50 moles of ions. This value of 2 x 0.25 is called the van't Hoff factor (i) and must be used whenever you calculate colligative properties of solutions containing ions.

Boiling Point Elevation:

Now that we have seen how addition of solutes to a solvent can lower its vapor pressure, let's see if we can figure out how this relates to the boiling point of the same solvent. The normal boiling point of a liquid is defined as the temperature at which the vapor pressure of the liquid is equal to standard pressure (1 atm). If we change the external pressure from 1 atm lower or higher, the boiling point changes as well. The boiling point is then simply the temperature at which the vapor pressure of the solvent equals the pressure of the surroundings. If you think about it, up until the vapor pressure reaches this point, the gas molecules cannot escape, right? The pressure on the surface is holding them in. Once you reach the boiling point temperature, the vapor pressure is then equal to the external pressure and the molecules can escape. Note that you really have to exceed the boiling point temperature to fully evaporate the liquid. I.e. steam is hotter than 100^oC.

Now back to colligative properties...how does adding solutes to a solvent affect the boiling point? Well, we now understand that solute molecules taking up positions at the surface of the liquid will depress the vapor pressure. We also know that we have to raise the vapor pressure of the liquid in order to reach the boiling point so this must mean we will have to input more energy to reach the same vapor pressure. Input of more energy equates to the input of heat in this type of system, so the boiling point temperature must be higher to obtain the same vapor pressure. Adding a non-volatile solute to a solution therefore raises the boiling point of that solution.

When a solute is dissolved in a solvent, the boiling point of the solution is raised according to the equation:

DT = iK_bm

DT= change in temperature
i = the van't Hoff factor, which is the number of particles into which the solute dissociates
m = the molality, which is the moles of solute per kilograms of solvent
K_b = the molal boiling point constant (for water, K_b = 0.5121^oC/m)

Want to practice some calculations using this equation? Click here.

Freezing Point Depression:

Let's start this discussion the same way we started the others, by defining the normal freezing point. The normal freezing point of a liquid is is the temperature at which a liquid becomes a solid at 1 atm. A more specific definition of freezing point is the temperature at which solid and liquid phases coexist in equilibrium. Let's see if we can figure out why the freezing point is lowered when we add solutes to a solution. We already know that in order to freeze a liquid, we have to lower the temperature. As the temperature lowers, the solution becomes more ordered as it moves toward the solid phase. This is an effect that works against the second law of thermodynamics. In short, entropy (disorder) likes to increase not decrease in the natural scheme of things. So if we have to lower the temperature to a certain point to freeze a pure solvent, when we add a solute we add to the entropy of the system, right? The mixture is more disordered than the pure. This additional amount of entropy must now be overcome to allow the liquid to change phases into a solid (become ordered). This means that the temperature will have to be even lower than before. Thus addition of any type of solute to a solvent will lower its freezing point.

As with boiling point elevation, the equation to figure out how great the change in temperature will be is given by:

DT = iK_fm

DT= change in temperature
i = the van't Hoff factor, which is the number of particles into which the solute dissociates
m = the molality, which is the moles of solute per kilograms of solvent
K_f = the molal freezing point constant (for water, K_f = -1.86 ^oC/m)

Want to practice some problems? Click here.

Using colligative properties to determine molecular weight of a substance:

Colligative properties such as freezing point depression or boiling point elevation can be used to calculate the molecular weight of a soluble solid.  To complete this calculation, the mass of solute and solvent must be known as well as the freezing points/boiling points of the pure solvent and the solution.

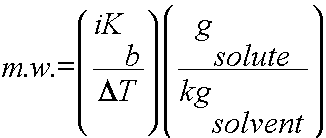    or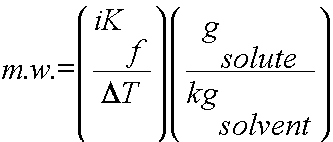    

Here are the steps to take:

1) Determine DT

2) Use DT, i and K_b or K_f to determine the molality of the solute (m = g_solute/kg_solvent).

3) Plug in all values and calculate for the m.w.

4) Use your common sense to assess your calculated value as reasonable or not! In other words, check for boo-boos.

Note: You can also use vapor pressure change or osmosis in the same manner to calculate molecular weight.