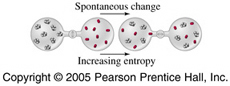
The direction of spontaneous change is the direction in which total entropy increases. Total entropy change, also called the entropy change of the universe, is the sum of the entropy change of a system and of its surroundings:
DSuniv = DSsys + DSsurr
According to the second law of thermodynamics, the entropy of the universe, Suniv must always increase for a spontaneous process, that is, DSuniv>0.

Free Energy and Free Energy Change—the Gibbs free energy, G, is used to describe the spontaneity of a process.
G = H - TDS
The free energy change, DG is equal to -TDSuniv and it applies just to a system itself, without regard for the surroundings. It is defined by the Gibbs equation:
DG = DH - TDS
For a spontaneous process at constant temperature and pressure, DG must be negative. In many cases, we can predict the sign of from the signs of DH and DS.
Standard Free Energy Change, DGo —the standard free energy change, DGo can be calculated (1) by substituting standard enthalpies and entropies of reaction and a Kelvin temperature into the Gibbs equation or (2) by combining standard free energies of formation through the expression
![]()
Summary of Gibbs free energy
Enthalpy change |
Entropy change |
Gibbs free energy |
Spontaneity |
positive |
positive |
depends on T, may be + or - |
yes, if the temperature is high enough |
negative |
positive |
always negative |
always spontaneous |
negative |
negative |
depends on T, may be + or - |
yes, if the temperature is low enough |
positive |
negative |
always positive |
never spontaneous |
Problems:
1) In the Haber process for the manufacture of ammonia
Equation |
Enthalpy change |
Entropy change |
|
N2 + 3H2 |
ΔH = -93Kj / mol |
ΔS = -198 j / mol K |
|
|
|
|
|
At what temperature will the reaction above become spontaneous?
The fact that both terms are negative means that the Gibbs free energy equation is balanced and temperature dependent:
ΔG = ΔH - TΔS
ΔG = -93000 - (T x -198) note that the enthalpy is given in kilojoules |
|
if ΔG = 0 then the system is at the limit of reaction spontaneity |
|
When ΔG = 0 then (T x -198) = -93000 |
|
and T = 93000/198 Kelvin |
|
therefore the reaction becomes spontaneous when T = 469 K (196 ºC) |
|
below this temperature the reaction is spontaneous.
2) Determine the Delta G under standard conditions using Gibbs Free Energies of Formation found in a suitable Thermodynamics table for the following reaction:
4HCN(l) + 5O2(g) ---> 2H2O(g) + 4CO2(g) + 2N2(g)
2 moles ( -237.2 kj/mole) = -474.4 kj = Standard Free Energy of Formation for two moles H2O(l)
4 moles ( -394.4 kj/mole) = -1577.6 kJ = Standard Free Energy of Formation for four moles CO2
2 moles(0.00 kj/mole) = 0.00 kJ = Standard Free Energy of Formation for 2 moles of N2(g)
(-474.4 kJ) + (-1577.6 kJ) + 0.00 = -2052 kJ = Standard Free Energy for Products
4 moles ( 121 kj/mole) = 484 kJ = Standard Free Energy for 4 moles HCN(l)
5 moles (0.00 kJ/mole) = 0.00 kJ = Standard Free Energy of 5 moles of O2(g)
(484) + (0.00) = 484 kJ = Standard Free Energy for Reactants
Sum of Free Energy of Products - Sum of Free Energy of Reactants = (-2052 kJ) - (484 kJ) = -1568 kJ = Standard Free Energy Change for the Reaction.
3) For the following reaction using the Thermodynamics table:
CoCl2(g) ---> CO(g) + Cl2(g)
Delta H = Sum of Delta Hf of products - Sum Delta Hf of Reactants
Delta H = [ 1(-110.5) + 1(0.00)] - [ 1(-220)]
Delta H = -110.5 - (-220) = +110.5 kJ
Delta S = Sum Standard Molar Entropies of Products - Sum of Standard Molar Entropies of Reactants
Delta S = [ 1 mole(197.5 J/mole-K) + 1 mole(223) J/mole-K] - [ 1 mole(283.7 J/mole-K)]
Delta S = 420.5 J/K - 283.7 J/K = 136.8 J/K
136.8 J/K X 1 kJ / 1000 J = 136.8 / 1000 = .1368 kJ/K
K = C + 273 = 127 + 273 = 400 K
Delta G = Delta H - T(Delta S)
Delta G = 110.5 kJ - 400 K(.1368 kj/K)
Delta G = 110.5 - 54.72 kJ = + 55.78 kJ
Because this reaction has a positive Delta G it will be non-spontaneous as written.
Name of Species Delta Hf(kJ/mole) Delta Gf(kJ/mole) S(J/mole-K)
CO2(g) -393.5 -394.4 213.7
CH3OH(l) -238.6 -166.2 127
COCl2(g) -220 -206 283.7
CO(g) -110.5 -137.2 197.5
C2H2(g) 227 209 200.9
Cl2(g) 0 0 223
HCN(l) 105 121 112.8
H2O(g) -241.8 -228.6 188.7
H2O(l) -285.8 -237.2 69.9
HNO3(aq) -206.6 -110.5 146
N2(g) 0 0 191.5
NO2(g) 33.2 51 239.9
NO(g) 90.3 86.6 210.7
O2(g) 0 0 205
CS2 151
H2 0 0 130.6
CH4 -74.8 -50.8 186.3
H2S -20.17 -33.01 205.6
SO2 248.1
Free Energy and Equilibrium.
Because DG is a measure of how favorable a reaction is, it also relates to the equilibrium constant.
DG =DGo + RT ln Q
Where Q is the same Q we used for calculating equilibrium (K is the special case for Q when at equilibrium.)
Starting with the change in free energy at constant temperature: DG° = DH° - TDS°, and with the relation between DG and equilibrium constant, K: DG° = -RT lnK, derive a linear equation that expresses lnK as a function of 1/T (a linear equation is of the form y = mx + b).
(b) The equilbrium constants for the conversion of 3-phosphoglycerate to 2-phosphoglycerate at pH 7 is provided:
T (°C) |
K |
0 |
0.1535 |
20 |
0.1558 |
30 |
0.1569 |
45 |
0.1584 |
Calculate DG° at 25°C.
(c) What is the concentration of each isomer of phosphoglycerate if 0.150 M phosphoglycerate reaches equilbrium at 25°C.
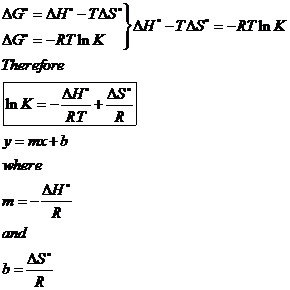
T(ºC) |
T(K) |
1/T(K-1) |
K |
lnK |
0 |
273 |
0.00366 |
0.1535 |
-1.874 |
20 |
293 |
0.00341 |
0.1558 |
-1.859 |
30 |
303 |
0.00330 |
0.1569 |
-1.852 |
45 |
318 |
0.00314 |
0.1584 |
-1.843 |
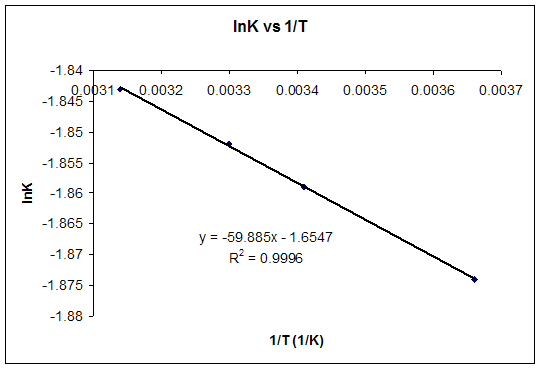
b) For T = 25ºC, using the equation of the graph, lnK = -1.8557 and K = 0.1564.
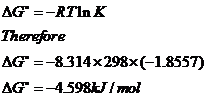
c)
