Chemical kinetics

Kinetics is the study of the rates of chemical processes.

The rate of a reaction is defined at the change in concentration over time:

Rate Expressions describe reactions in terms of the change in reactant or product concentrations over the change in time. The rate of a reaction can be expressed by any one of the reactants or products in the reaction.

There are a couple of rules to writing rate expressions:

1) Expressions for reactants are given a negative sign. This is because the reactant is being used up or decreasing.

2) Expressions for products are positive. This is because they are increasing.

3) All of the rate expressions for the various reactants and products must equal each other to be correct. (This means that the stoichiometry of the reaction must be compensated for in the expression)

Example: In an equation that is written: 2X + 3Y —> 5Z

The Rate Expression would be: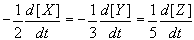

The Mathematical way of looking at it: The rate may vary with time (and concentration), so it is usual to define the rate over a very small time, Δt. We think of the rate as the derivative of concentration with respect to time: This derivative is the slope of a graph of concentration against time, taken at a particular time. On the graph, an exponential fit is used to create a best fit line that will allow you to calculate the rate at any point.

We have already established that a change in concentration can affect the rate at which a reaction proceeds (collision theory). As a reaction progresses,the concentrations of both reactants and products change and thus the rate of the reaction changes. This also means that the rate of a reaction can be expressed in terms of the diminishing concentrations of its reactants or the increasing concentrations of its products. The expressions used to describe these relationships are called Rate Laws or Rate Equations.

Three ways to quantitatively determine rate:

Initial Rate: The Method of Initial Rates involves measuring the rate of reaction, r, at very short times before any significant changes in concentration occur. A + 2B --> 3C

While the form of the differential rate law might be very complicated, many reactions have a rate law of the following form: r = k [A]^a[B]^b

The initial concentrations of A and B are known; therefore, if the initial reaction rate is measured, the only unknowns in the rate law are the rate constant, k, and the exponents a and b. One typically measures the initial rate for several different sets of concentrations and then compares the initial rates.

The exponents a and b are the "orders" of the rate equation and they must be determined experimentally. The overall order of a reaction is determined by adding up the exponents. I.e. If a=1 and b=2, the reaction is third order overall.

1. 1st-order reactions
   • Reactions in which the rate varies with concentration of a single species, and the change in concentration is exponential, so that a plot of ln(concentration) v. time is linear. The stoichiometric coefficient is 1. Radioactive decay is an example usually cited, but many electron transfer processes, and most enzyme mechanisms contain intermediate reactions that are first order.
2. 2nd-order reactions of Class I
   • Reactions in which the rate varies with concentration of a single species, but the stoichiometric coefficient is 2. The rate varies with the reciprocal of the concentration, so that a plot of 1/(concentration) v. time is linear.
3. 2nd-order reactions of Class II
   • Reactions in which the rate varies with the concentration of two substrates, each of which has a stoichiometric coefficient of 1. A plot of ln(conc.A/conc.B) v. time is linear.
4. Higher-order reactions
   • Reactions in which more than two species are involved, or one species reacts with stoichiometric coefficient >2. Many different classes, of which the simplest involves a single species with stoichiometric coefficient greater than 2. Although many biochemical reactions might appear to be higher-order, in general, the enzyme mechanism functions through binding of multiple substrates to a single protein, and the empirical order is simpler, and often appears to be zero-order (see below).
5. Zero-order reactions
   • Many reactions in biochemistry appear to occur at a rate independent of substrate concentration. These are said to show zero-order behavior. In general, this is because the reaction is enzyme-catalyzed, and the rate is determined by the concentration of enzyme, as long as the substrate is in excess, so that the rate is saturated.

Consider the following set of data:

If simple multiples are chosen for the concentrations and only one concentration is varied at a time, one can determine a and b by inspection. In this case the values of a and b may not be obvious. One can employ the following algebraic technique for determining the exponents.

Step 1) First, write the ratio of the rate laws for two trials.

Step 2) Next, substitute the numerical values into the equation.

Step 3) Algebraically simply where you can.

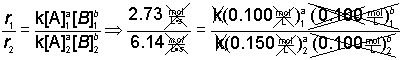
Step 4) To convert a from an exponent into a coefficient, take the logarithm of both sides of the equation.

a = 1.9995 = ~2

Average Rate: Calculates the rate over the whole time of the reaction.

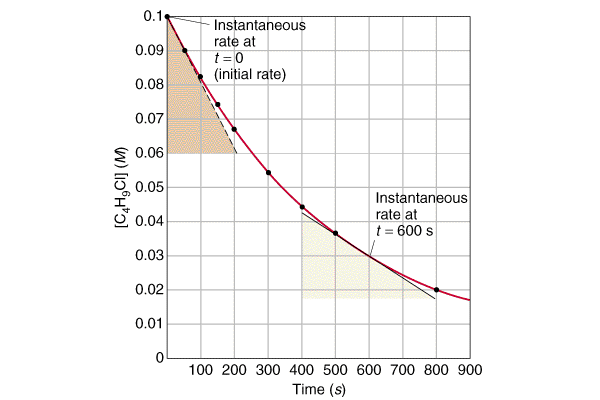
Instantaneous Rate: Rate decreases over time. Therefore instantaneous rate, the rate at any given time, is sometimes used. The instantaneous rate can be determined from a tangent line at the relevant instant of time on a graph of concentration versus time.

A comparison of the methods demonstrates the strengths and weakness of each:

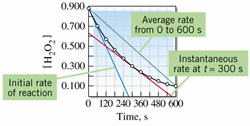
Note that none of the three methods actually yields a true picture of the changing rate of the reaction.

Integrated Rate Law:

Consider the reaction A --> B

The rate of reaction, r, is given by

Suppose this reaction obeys a first-order rate law: r = k [A]

This rate law can also be written as:

Rearrange

and then integrate. At t = 0, the concentration of A is [A]₀. The integrated rate law is thus:

Summary of the Integrated Rate Expressions:

Graphically Determing the Order:

Need Practice? Here is a test bank with lots of self-grading questions to help you learn: http://lrc-srvr.mps.ohio-state.edu/under/chemed/qbank/quiz/bank10.htm