What is Vaporization?

Vaporization is the process of converting a liquid into a gas. It is also called evaporation. Since we know that the particles of a gas are moving faster than those of a liquid, an input of energy must be required for a liquid to become a gas. The most common way to add energy to a liquid system is by adding heat.

As a liquid gains energy, the molecules begin to move around faster. If a molecule is on the surface of the liquid, and has enough energy, it can break free and become a gas molecule. As with anything in chemistry, or life for that matter, there are other factors that determine how easily a molecule can break free from the liquid. We just discussed some of them: intermolecular forces.

The stronger the intermolecular forces that are holding a liquid together, the more energy that will be required to pull them apart. What this means in practicle terms is that a liquid with strong intermolecular forces will have to be heated to a higher temperature before it will evaporate.

For example: Look at Methane (CH₄ M.W. 16 g/mol) and Water (H₂O 18 g/mol). Their molecular weights are very similar, but their Heats of Vaporization (how much heat per mole that has to be added to make them evaporate) are very different. Water has a DH_vap of 40.7 kJ/mol and Methane has a DH_vap of 8.2 kJ/mol. Methane is actually a gas at room temperature because of its low heat of vaporization.

What is condensation?

Well, the opposite of vaporization, of course. The process by which a gas changes phases into a liqud. And if you must add energy/heat a liquid to convert it to a gas, then you must remove energy from or cool a gas to convert it into a liquid. Make sense? Yes. What else makes sense is that the amount of energy required to go from gas to liquid phase would be the same as that required to go from liquid to gas, just opposite in sign. So the Heat of Vaporization is the same for both processes, just positive (endogonic/endothermic) for evaporation and negative (exergonic/exothermic) for condensation.

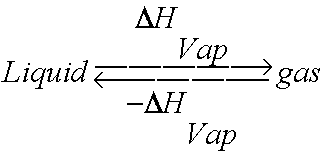
Another property that affects the value of the DH_vap is the molecular weight or size of the molecule. This is generally because you have more surface (London Force) interactions between larger molecules than small and the density of a larger molecule is generally greater than that of a small molecule. Remember, that to become airborne a molecule must have a lower density than the air molecules around it. So as a general trend, as the MW/size of a molecule increases so will the DH_vap. Exceptions in the trend will occur when a small molecule is capable of a stronger intermolecular force, E.g. HF versus HBr. HF hydrogen bonds and thus has a higher DH_vap.

So now that you know all about what a DH_vap is, why the heck do we care about it? Well, here is a real life use for this value that is important to us all: fingernail polish drying times. For fingernail polishes, if you want the polish to dry faster, you use a solvent that has a lower DH_vap. For example: Table 2 lits some of the more common solvents used in fingernail polishes. Methyl Acetate is the preferred solvent for most. This is because not only is it fast drying, it is also somewhat water soluble.

Another simple example of how to use the value is determing how much heat it will take to boil water out of a pot? The DH_vap for water is 40.7 kJ/mol. If your pot contains 2.2 liters of water and we assume the density of the water is ~1g/mL then the mass of the water in the pot is 2.2 x 10³ grams. The molecular weight of water is 18.0 g/mol so this means we have 2.2 x 10³ grams/18.0g/mol = 122.2 moles of water. We can now use the 40.7 kJ/mol factor to show that it will take 122.2 mol x 40.7 kJ/mol = 4974.4 kJ of energy to evaporate all of the water in the pot.

What if we take it one step further? Let's combine some concepts we learned in CHM1045 with the concept we just discussed and solve the following problem: How much heat energy is required to convert
5.00 kg of ice at 0°C, into 5.00 kg of steam at 100.°C?

What do we need to calculate? First we need convert the ice from solid to liquid using the Enthalpy of Fusion (a value just like the Heat of Vaporization that measures the amount of heat required to convert a substance from solid to liquid) and then we need to heat the material from 0 up to 100 degrees and finally, we need to convert it from liquid to gas using the Heat of Vaporization.

So now we know the three steps to take, we need to collect our conversion factors to use:

Step 1: Melt the solid ice, for this we need to know the DH_fus of the ice which is 335 kJ/kg. So we can simply multiply the number of kg in our

Step 2: We need to heat the liquid water from 0 to 100 degrees Celsius. The energy (q) required to do this can be calculated using q= mcDT, where m is the mass of the water, DT is the Change in temperatue and c is the specific heat of water (a CHM1045 concept that descibes how much heat energy a substance can absorb before it rises in temperature one degree). The specific heat of water is 4.19 J/g^oC .

Step 3: Convert the liquid water into vapor at 100 ^oC. For this we use the Heat of Vaporization as we did above. (Note: If you convert the units of the DH_Vap from kJ/mol to kJ/kg you get ~2300 kJ/kg)

What is Vapor Pressure?

Vapor pressure is a measurable quantity that exists when a liquid and its vapor are in equilibrium. This is only possible in closed systems. But please note that the earth's atmosphere is considered a closed system. On a much smaller scale this would be when you place any liquid into a sealed container. The molecules at the surface of the liquid would be changing into gas phase molecules and returning to the liquid until an equilibrium was reached. This is what we call a "dynamic equilibrium". As molecules from the liquid move into the gas phase within the container, this increases the pressure above the liquid. A measure of this pressure (minus the normal atmospheric pressure) gives us the vapor pressure of the liquid. The higher this pressure, the more volatile a liquid is said to be. Vapor pressure is also dependent on the temperature of the system. The liquid will still have a heat of vaporization to contend with so the equilibrium vapor pressure will increase at higher temperatures.( And anyone who has ever microwaved their lunch in a closed tuperware container knows what will happen if the pressure or temperature gets too high, don't they?)

Practical use of the vapor pressure numbers:

You are going away for the weekend and you want to make sure you leave enough water in the cage for your bird so it doesn't die of thirst while you are gone. If your dorm room has an average temperature of 21^oC how many liters of water should you put out to be sure some remains for the entire weekend?

Well, at 21^oC the vapor pressure of water is ~18 mmHg. If we assume your dorm room has a volume of about 5.0 x 10⁴ L, we can use the ideal gas law to determine how much water will evaporate and just make sure more than that is available for the bird.

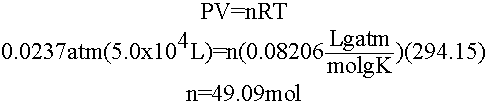
49.09 moles of water is only about 883 g of water or ~883 mL so if we leave anything in excess of this for the bird it won't evaporate and the bird will be fine!

A couple of things to note about the calculation above: 1) If the room were bigger, more water would need to evaporate before the equilibrium vapor pressure was met and 2) if the temperature was higher in the room the equilibrium vapor pressure would be higher as well. Vapor pressure is temperature dependent!

So for practical use, we would need to know how the vapor pressure changed with temperature (that way you can leave your bird at someone else's house, yeah! even if their place doesn't have air conditioning). Unfortunately, we quickly see that most vapor pressure relationships with temperature are not linear, which makes predictions difficult if not impossible. Boo!

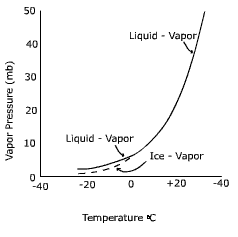
Never fear, Clausius-Clapeyron is here! A German and Frenchman walked into a bar... uh no, that is another story. Anyway, A German Physicist named Clausius got together with a French physicist named Clapeyron and devised a neat little equation that converts the non-linear relationship between vapor pressure and temperature into a linear one using the pressures and temperatures of a substance at two points.

The Clausius-Clapeyron Equation:

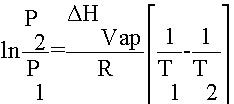
Basically, you can use this equation for a number of different purposes: 1) You can calculate the Heat of Vaporization for a substance by measuring its temperature and pressure twice. 2) You can determine the vapor pressure of a substance at any temperature as long as you know it DH_vap and the temperature and pressure at another point.

The biggest problem students have with this equation is their inability to complete the mathematical manipulations that go along with its solutions. In order to practice some problems, click here.

And a few more definitions:

Boiling Points:

The boiling point of a liquid is the temperature at which the liquid will convert to a gas. If the atmospheric pressure at this temperature is given as 1 atmosphere or 760 mmHg, then this temperature is called the normal boiling point of the liquid. Boiling points are therefore pressure dependent. (The lower the atmospheric pressure, the lower the boiling point and vice versa). This is because the atmospheric pressure is what is pushing against the surface of the liquid and keeping the liquid down. When the vapor pressure of the liquid is equal to or greater than the atmospheric pressure, boiling will occur (or in other words vapor will form) and the gas phase molecules will escape from the surface of the liquid (you see this as bubbles).

Critical Temperature and Pressure:

The temperature and pressure at which the line between liquid and gas phase blurs is called the critical temperature and critical pressure, respectively. At very high temperatures and pressures the properties of a substance resemble those of both a liquid and a gas.

Supercritical Fluids:

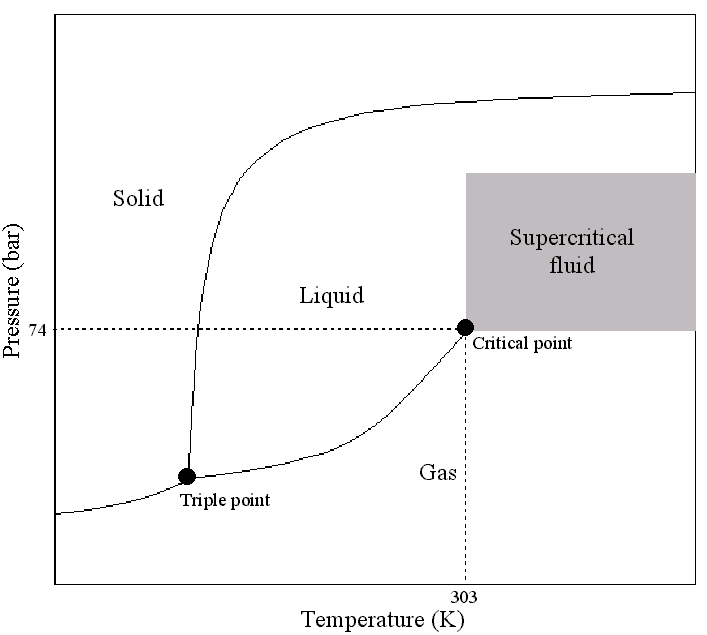
A Super Critical Fluid (SCF) is defined as a substance above its critical temperature (TC) and critical pressure (PC). The critical point represents the highest temperature and pressure at which the substance can exist as a vapour and liquid in equilibrium. The phenomenon can be easily explained with reference to the phase diagram for pure carbon dioxide (Figure below). This figure shows the areas where carbon dioxide exists as a gas, liquid, solid or as a SCF. The curves represent the temperatures and pressures where two phases coexist in equilibrium (at the triple point, the three phases co-exist). The gas-liquid coexistence curve is known as the boiling curve. If we move upwards along the boiling curve, increasing both temperature and pressure, then the liquid becomes less dense due to thermal expansion and the gas becomes more dense as the pressure rises. Eventually, the densities of the two phases converge and become identical, the distinction between gas and liquid disappears, and the boiling curve comes to an end at the critical point. The critical point for carbon dioxide occurs at a pressure of 73.8 bar and a temperature of 31.1°C.

Surface Tension:

Molecules on the surface of a liquid are held to the liquid by the intermolecular attractions from the molecules below and beside them. Surface tension has units of erg/cm² or dyne/cm. It arises because atoms on the surface are missing bonds. Energy is released when bonds are formed, so the most stable low energy configuration has the fewest missing bonds. Surface tension therefore tries to minimize the surface area, resulting in liquids forming spherical droplets and allowing insects to walk on the surface without sinking.

Capillary Action:

Capillary action is a physical effect caused by the interactions of a liquid with the walls of a thin tube. The capillary effect is a function of the ability of the liquid to wet a particular material. The liquid for which this effect is most commonly seen is water, because water is capable of strong surface interactions and because water is ubiquitous.

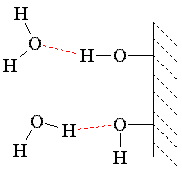Water climbs up a thin glass tube because of the strong hydrogen-bonding interactions between the water and the oxygens (and terminal hydrogens) at the surface of the glass (SiO2; surface oxygens are typically bonded to hydrogen). The energetic gain from the new intermolecular interactions must be balanced against gravity, which attempts to pull the liquid back down. Therefore, the narrower the tube, the higher the liquid will climb, because a narrow column of liquid weighs less than a thick one. This is the process by which plants absorb moisture from the soil.

Viscosity:

Viscosity is an internal property of a fluid that offers resistance to flow.