Programming Projects: DIIS convergence acceleration in SCF
Overview
Often, the convergence of the SCF procedure outlined in the previous projects is disappointingly slow. Fortunately, many convergence acceleration procedures have been developed, and, in this tutorial, you will implement one of the most popular: the direct inversion of the iterative subspace (DIIS). This tutorial is based upon the DIIS procedure described by Peter Pulay here.
This tutorial assumes you have already developed a working Hatree-Fock code, based on one of these tutorials.
The C++ code for the DIIS-accelerated SCF plugin can be found here. The C++ code and corresponding header for the DIIS manager class can be found here and here, respectively.
Procedure:
The basic idea of DIIS is simple. In the course of an SCF optimization, we have a series of approximate solution vectors (e.g. orbitals, densities, or Fock matrices). For each approximate solution vector, we can define an associated error vector. In DIIS, we choose an extrapolated solution vector as a linear combination of previous vectors, and the coefficients are chosen in a way that minimizes the error associated with the new vector.
Step 1. Develop a Hartree-Fock code
You must first develop your own Hartree-Fock SCF plugin to Psi4. You can base your plugin off of either of these tutorials. The notation used below is consistent with that used in those tutorials.
Step 2. Choose the Fock matrix as the current solution vector
Once we begin the SCF iterations, the parameter that we will extrapolate will be the Fock matrix (in the orthonormal basis):
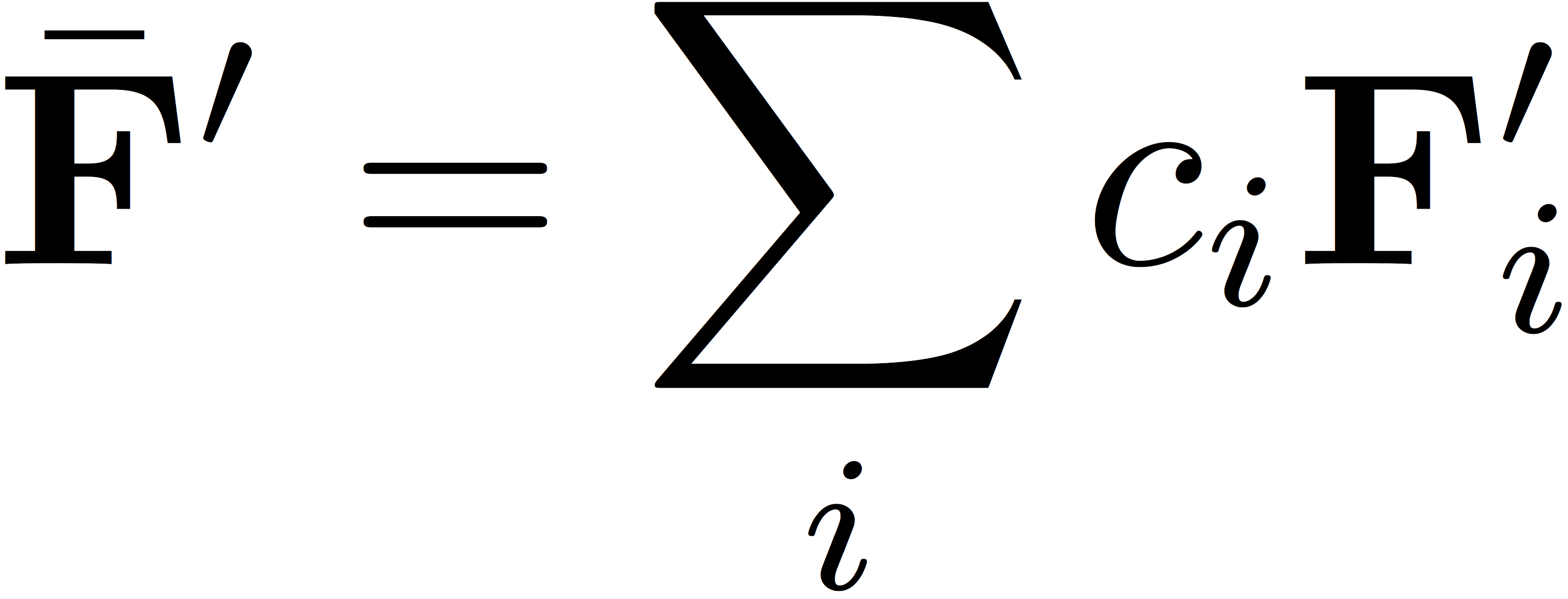
The coefficients, ci, will be chosen such that the error associated with the extrapolated Fock matrix will tend to zero
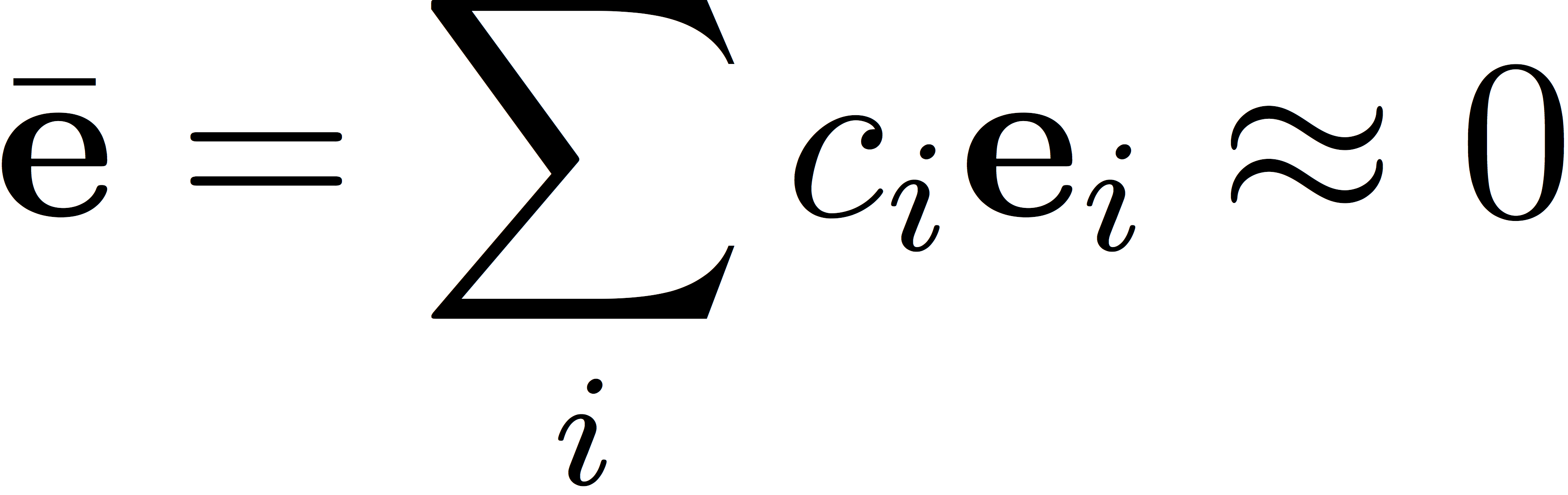
We will also require that the coefficients sum to one
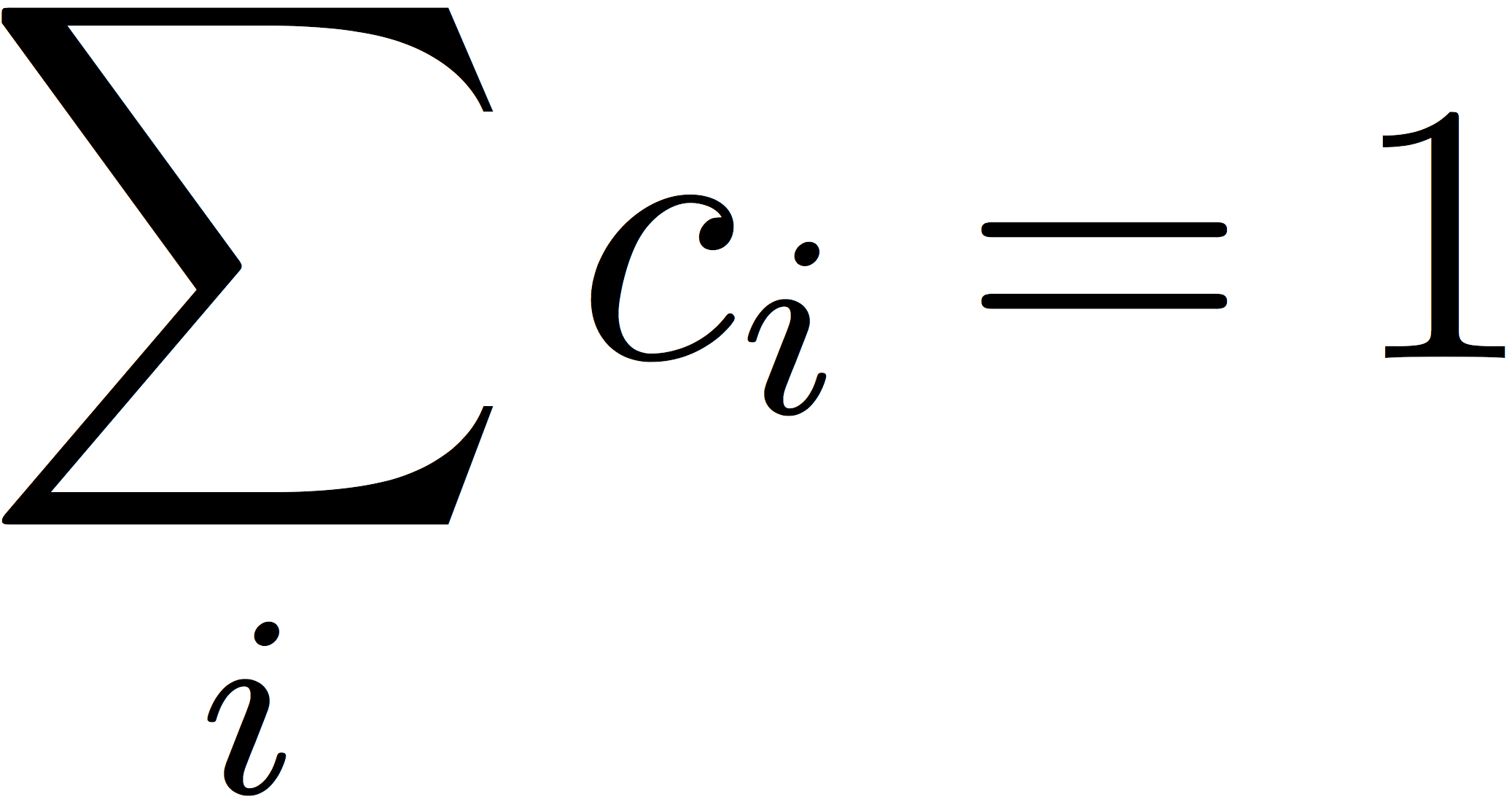
In general, this extrapolation should involve a small number of vectors, and you can store these matrices in main memory or on disk. The DIIS manager class given here stores eight solution and error vectors on disk.
Step 3. Choose an error vector
There are many possible definitions of the error vectors. For example, we could simply choose the change in the Fock matrix each iteration as an estimate of the error. Pulay proposed that the error vector should be given by the commutator of the Fock and density matrices (the orbital gradient) FiDiS-SDiFi, where Fi and Di are the Fock and density matrices at iteration i (in the AO or SO basis), and S is the overlap matrix. In the orthonormal basis defined by Löwdin's symmetric orthogonalization we have
As with the current solution vectors (the Fock matrices), we store a small number (eight) of error vectors. Again, you can store these in main memory or on disk.
Check your error vector from the first SCF iteration.
Step 4. Determining the coefficients, ci
Once you have accumulated at least two solution and error vectors, you can determine the coefficients, ci. The coefficients are chosen such that they minimize the norm of the extrapolated error vector
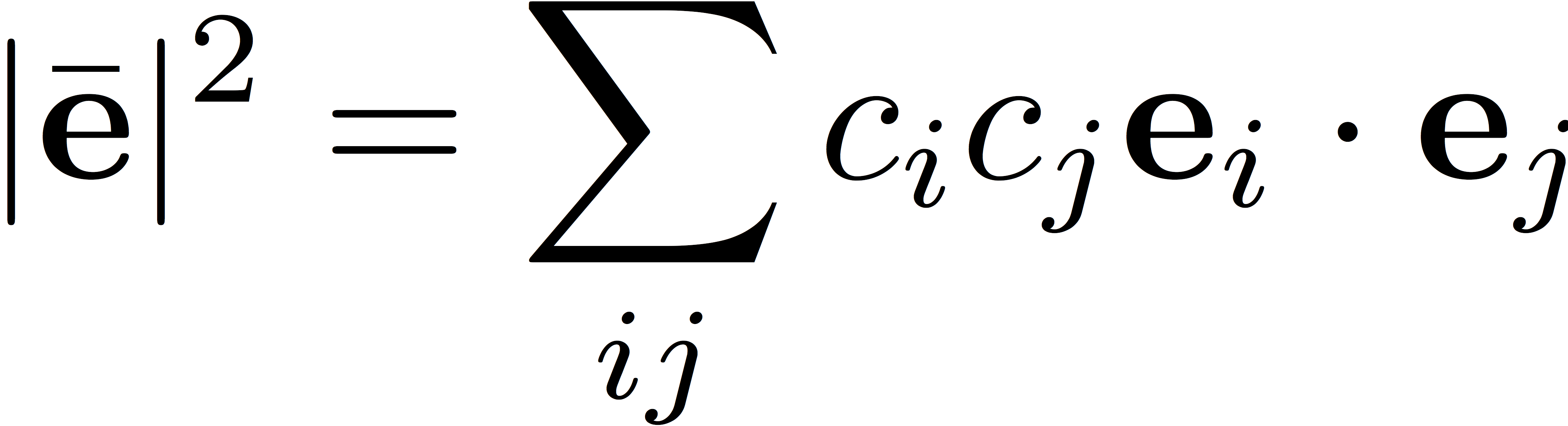
To find the coefficients, we use the method of Lagrange multipliers. We define the Lagrangian
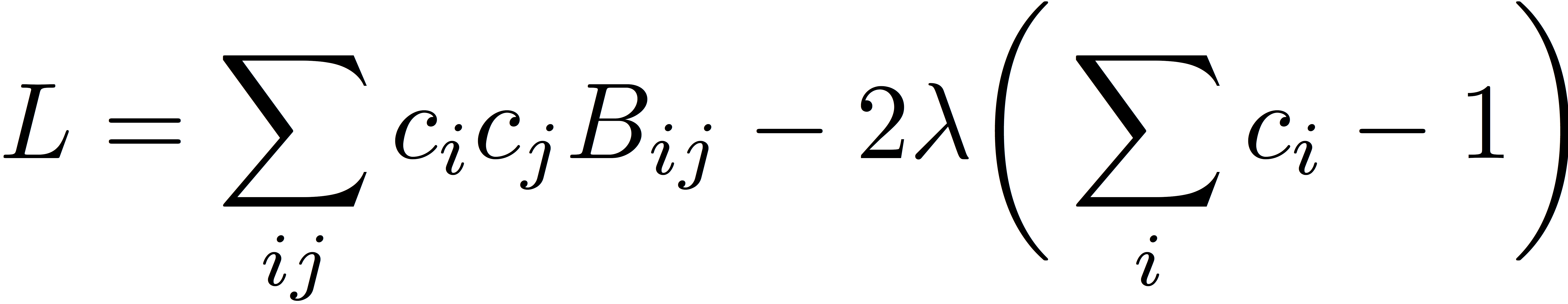
where
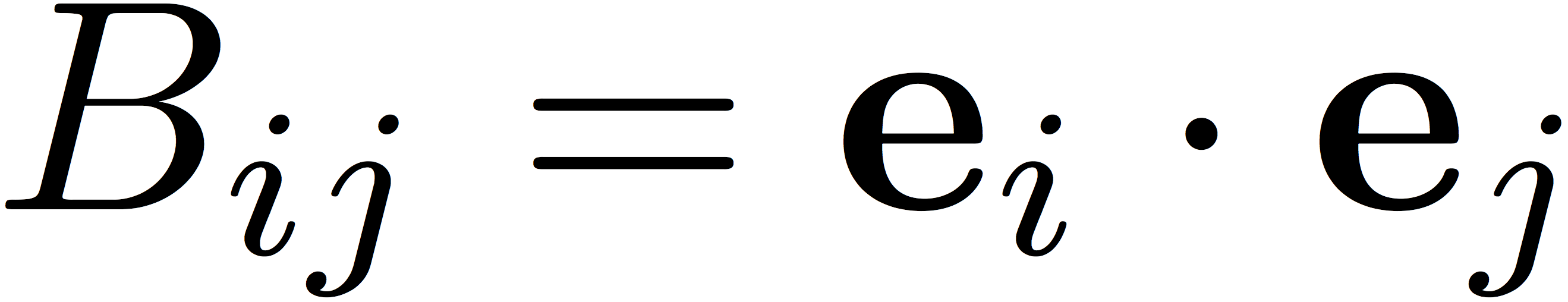
are elements of the error matrix, and λ is the Lagrange multiplier for the constraint that the coefficients sum to one. The extra factor of two in the Lagrangian is introduced for convenience and has no effect on the optimal value of the coefficients, ci. We arrive at the following system of equations when we require that the Lagrangian be stationary with respect to variations in all of the coefficients and the Lagrange multiplier.
In your Psi4 plugin, you can solve this system of equations using the LAPACK routine DGESV. To do so, include the following header file:
#include "psi4/libqt/qt.h"You can then use the function C_DGESV. For the call structure for C_DGESV, see lapack_intfc.cc.
Note that the computational cost of the construction of the error matrix can be reduced by recognizing (i) the matrix is symmetric so only the lower or upper triangle need be computed and (ii) only one row/column must explicitly be computed each iteration. The remainder of the matrix can be stored (in memory or on disk) and reused iteration to iteration.
Check your coefficients from the first DIIS extrapolation.
Step 5. Extrapolate the Fock matrix
Once you have determined the coefficients, ci, extrapolate the Fock matrix according to
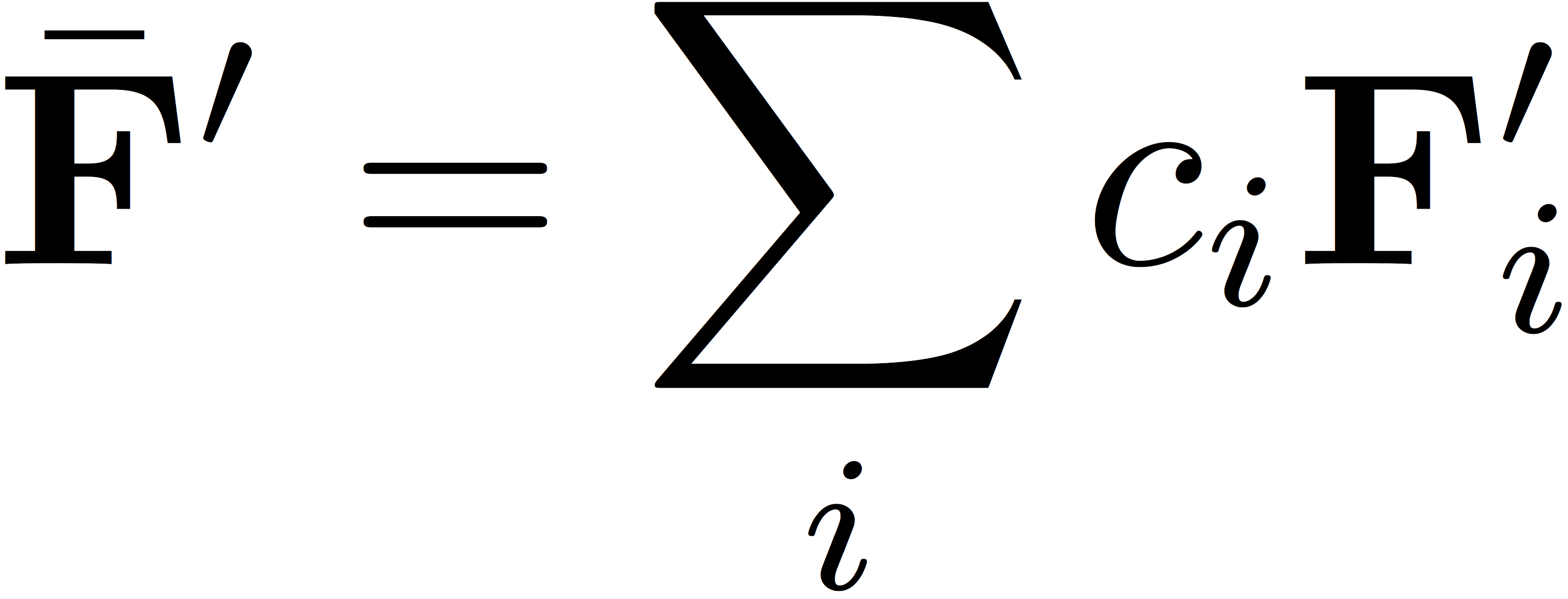
Now, we resume the Hatree-Fock procedure. Diagonalize the extrapolated Fock matrix to determine its eigenvectors (the molecular orbitals, C') and eigenvalues (the molecular orbital energies, ε)
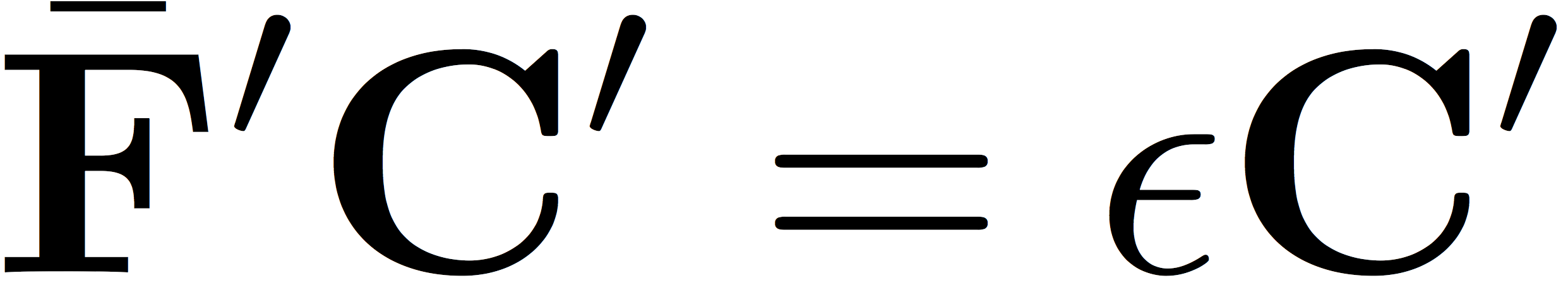
As in the previous tutorials, back transform one index of C' to the original AO basis in order to build the density matrix for the next iteration:
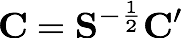
Step 6. Replacing solution and error vectors
Since only a small number of solution and error vectors (e.g eight) are used in the extrapolation procedure, we will need to replace some of the older vectors as the SCF procedure goes beyond eight iterations. You can choose to replace either the oldest vectors or those vectors with the largest associated error vector. Our DIIS manager replaces the vector with the largest associated error.
Step 7. Monitoring convergence
In our previous tutorials, the SCF procedure was considered converged when changes in energy and density between iterations fell below some predefined thresholds. Here, we use the change in the energy and the the root-mean square (RMS) orbital gradient to measure convergence.
Consider the Hartree-Fock procedure for the same molecule/basis set combinations used in the previous tutorials. Without DIIS, the energy and orbital gradient should converge to 12 decimal places in about 28 iterations:
Guess energy: -118.308230720196
==> Begin SCF Iterations <==
Iter energy dE RMS |[F,P]|
0 -73.196938802615 45.111291917580 0.161149650787
1 -74.939192979935 -1.742254177320 0.012516596135
2 -74.944687307745 -0.005494327810 0.002868867004
3 -74.945047846381 -0.000360538636 0.000948342720
4 -74.945095717316 -0.000047870934 0.000366501367
5 -74.945103245253 -0.000007527938 0.000147962847
6 -74.945104500848 -0.000001255594 0.000060823893
7 -74.945104714602 -0.000000213755 0.000025151359
8 -74.945104751242 -0.000000036639 0.000010420756
9 -74.945104757536 -0.000000006294 0.000004320278
10 -74.945104758618 -0.000000001082 0.000001791480
11 -74.945104758804 -0.000000000186 0.000000742916
12 -74.945104758836 -0.000000000032 0.000000308089
13 -74.945104758842 -0.000000000006 0.000000127766
14 -74.945104758842 -0.000000000001 0.000000052985
15 -74.945104758843 -0.000000000000 0.000000021973
16 -74.945104758843 0.000000000000 0.000000009112
17 -74.945104758843 0.000000000000 0.000000003779
18 -74.945104758843 -0.000000000000 0.000000001567
19 -74.945104758843 0.000000000000 0.000000000650
20 -74.945104758843 0.000000000000 0.000000000270
21 -74.945104758843 0.000000000000 0.000000000112
22 -74.945104758843 0.000000000000 0.000000000046
23 -74.945104758843 0.000000000000 0.000000000019
24 -74.945104758843 0.000000000000 0.000000000008
25 -74.945104758843 0.000000000000 0.000000000003
26 -74.945104758843 -0.000000000000 0.000000000001
27 -74.945104758843 0.000000000000 0.000000000001
SCF iterations converged!
* SCF total energy: -74.945104758843
For the same convergence thresholds, DIIS reduces the number of iterations to only nine:
Guess energy: -118.308230720196
==> Begin SCF Iterations <==
Iter energy dE RMS |[F,P]|
0 -73.196938802615 45.111291917580 0.161149650787
1 -74.939192979935 -1.742254177320 0.012516596135
2 -74.944687307745 -0.005494327810 0.002868867004
3 -74.945059469653 -0.000372161908 0.000830998716
4 -74.945103419151 -0.000043949498 0.000142890940
5 -74.945104756790 -0.000001337639 0.000006828537
6 -74.945104758843 -0.000000002052 0.000000068811
7 -74.945104758843 -0.000000000000 0.000000000398
8 -74.945104758843 0.000000000000 0.000000000000
SCF iterations converged!
* SCF total energy: -74.945104758843
If we double the O-H bond length
molecule {
O
H 1 R
H 1 R 2 A
R = 1.8
A = 104.5
# add this line!
symmetry c1
}
we find that the basic SCF procedure does not converge:
Guess energy: -116.837914524518
==> Begin SCF Iterations <==
Iter energy dE RMS |[F,P]|
0 -73.226880190015 43.611034334503 0.037704098895
1 -73.362990265269 -0.136110075254 0.068817042077
2 -73.553585133343 -0.190594868074 0.076418280252
3 -73.590354082648 -0.036768949305 0.082674491025
4 -73.682157222699 -0.091803140051 0.082580895233
5 -73.678727769308 0.003429453391 0.085365751694
6 -73.735922659086 -0.057194889778 0.084107422060
7 -73.717253914233 0.018668744853 0.086133433309
8 -73.760261977557 -0.043008063324 0.084608450174
9 -73.735037381968 0.025224595589 0.086406150756
10 -73.771698133826 -0.036660751858 0.084803784715
11 -73.743474775749 0.028223358077 0.086517537730
12 -73.777171073830 -0.033696298081 0.084888261557
13 -73.747532013052 0.029639060777 0.086566973068
14 -73.779813873486 -0.032281860434 0.084926973128
15 -73.749495788237 0.030318085249 0.086589937774
16 -73.781095646346 -0.031599858109 0.084945260963
17 -73.750449319650 0.030646326696 0.086600861938
18 -73.781718642130 -0.031269322479 0.084954034686
19 -73.750913034440 0.030805607690 0.086606120963
20 -73.782021759446 -0.031108725006 0.084958276341
21 -73.751138715146 0.030883044300 0.086608667749
22 -73.782169315262 -0.031030600116 0.084960334716
23 -73.751248589775 0.030920725488 0.086609904671
24 -73.782241162329 -0.030992572554 0.084961335442
25 -73.751302092769 0.030939069560 0.086610506272
26 -73.782276149910 -0.030974057141 0.084961822407
27 -73.751328148099 0.030948001811 0.086610799076
28 -73.782293188914 -0.030965040815 0.084962059474
29 -73.751340837277 0.030952351637 0.086610941634
30 -73.782301487171 -0.030960649894 0.084962174909
31 -73.751347017148 0.030954470023 0.086611011053
32 -73.782305528605 -0.030958511458 0.084962231124
33 -73.751350026892 0.030955501713 0.086611044860
34 -73.782307496887 -0.030957469994 0.084962258500
35 -73.751351492717 0.030956004170 0.086611061324
36 -73.782308455493 -0.030956962776 0.084962271833
37 -73.751352206614 0.030956248879 0.086611069342
38 -73.782308922361 -0.030956715747 0.084962278327
39 -73.751352554301 0.030956368059 0.086611073248
40 -73.782309149738 -0.030956595437 0.084962281489
41 -73.751352723635 0.030956426103 0.086611075149
42 -73.782309260478 -0.030956536843 0.084962283029
43 -73.751352806106 0.030956454372 0.086611076076
44 -73.782309314411 -0.030956508306 0.084962283779
45 -73.751352846271 0.030956468140 0.086611076527
46 -73.782309340678 -0.030956494407 0.084962284145
47 -73.751352865833 0.030956474845 0.086611076747
48 -73.782309353471 -0.030956487638 0.084962284323
49 -73.751352875360 0.030956478111 0.086611076854
50 -73.782309359701 -0.030956484342 0.084962284409
Without DIIS, the SCF procedure appears to oscillate between two different solutions. On the other hand, SCF with DIIS converges nicely in only 15 iterations:
Guess energy: -116.837914524518
==> Begin SCF Iterations <==
Iter energy dE RMS |[F,P]|
0 -73.226880190015 43.611034334503 0.037704098895
1 -73.362990265269 -0.136110075254 0.068817042077
2 -73.553585133343 -0.190594868074 0.076418280252
3 -74.464883669436 -0.911298536093 0.032080900797
4 -74.429023374665 0.035860294771 0.041606480071
5 -74.456614357821 -0.027590983157 0.034310669154
6 -74.511256860259 -0.054642502438 0.000395057332
7 -74.511195829728 0.000061030531 0.001422608517
8 -74.511030534112 0.000165295616 0.002554059031
9 -74.511052613564 -0.000022079452 0.002456520204
10 -74.511052329069 0.000000284495 0.002457817744
11 -74.511322873032 -0.000270543963 0.000008732217
12 -74.511322876759 -0.000000003727 0.000000074001
13 -74.511322876760 -0.000000000000 0.000000000420
14 -74.511322876760 0.000000000000 0.000000000001
SCF iterations converged!
* SCF total energy: -74.511322876760
You can check your expansion coefficients, F' matrices, or error vectors for this case.
We should note here that there are other methods, such as level shifting, that can improve the convergence of SCF in divergent cases without the use of DIIS.






