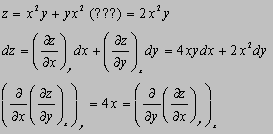
HOMEWORK #4
SOLUTIONS
September 21, 1998
Chapter 3, Exercises #3.4(b), 3.11(b), 3.12(b), 3.13(b); Problems #3.1, 3.2
Chapter 4, Exercises #4.1(b), 4.3(b), 4.5(b), 4.6(b)
3.4(b)
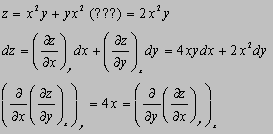
3.11(b)
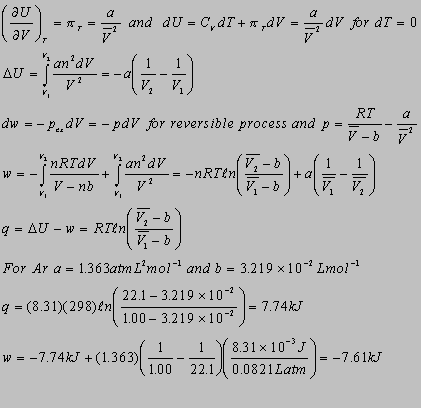
3.12(b)
V = V[0.77 + 3.7x10-4T + 1.52x10-6T2]
= (1/V)(V/T)p = (1/V)(V[3.7x10-4 + 3.04x10-6T]
=[3.7x10-4 +3.04x10-6T]/[0.77 + 3.7x10-4T
+ 1.52x10-6T2] = 1.273x10-3/K at 310K
3.13(b)
= -(1/V)(V/p)T = 2.21x10-6 /atm
= m/V (/p)T = (-m/V2)(V/p)T from the
chain rule and
= (m/V)(-1/V)(V/p)T =
Thus d/ = dp and integrating, n(2/1) = (p2 - p1) = p
For the density to increase by 8% implies that 2 = 1.081
p = n(1.08)/2.21x10-6 = 3.48x104 atm p2
(That is, p1 is only 1 atm.)
3.1
= 2.21x10-6 atm-1 (1atm/1.01x105Pa)
= 2.19x10-11Pa-1
at 1.000 km, p = gh = (1.03g/cm3)(1m3/106cm3)(10-3kg/1g)(9.81m/s2)(1000m)
= 1.01x107Pa
dV/V = -dp at constant T. Thus, n(V2/V1) = -p,
and V2 = V1exp(-p).
V2 = (103cm3)exp(-2.19x10-11Pa-1
x 1.01x107Pa) = 999.8cm3
Since dV = VdT - Vdp, we can fix T and change p; and then fix p and
change T, since V is a state function:
(Assuming that and are constants) n(V2/V1) = T
and V2 = V1exp(T)
Thus, the new V2 = 999.8exp(8.61x10-5K-1
x 30K) = 997.2cm3
3.2
There are several ways to approach this problem depending on the data available. For example, for this process at constant p: dH = CpdT and dU = CVdT + TdV. Since dV = VdT - Vdp = VdT at constant p, dU = (CV + TV)dT. Or, one can find U from U = H -(pV).
Using the second method, dH = CpdT or H = CpT
for constant Cp = 75.291J/mol-K from Table 2.6. Thus H = 752.91
for a 10K increase in T.
U = H - p(V2 - V1) where p = 1 bar = 105Pa.
Since dV = VdT at constant pressure or n(V2/V1) = T, then
(V2 -V1) = V1(exp(T) - 1) = 18cm3(exp(2.1x10-4(10))
- 1) = 18(2.1x10-3)
and U = 752.91J - 105Pa(18cm3)(1m3/106cm3)(2.1x10-3)
= 752.91-0.003 = 752.91J
The small difference in energy and enthalpy for this small temperature
increase is due to the work that is done by thermal expansion of the water
as it is warmed by 10 degrees.
4.1(b)
dS = dqrev/T
a) S = 50kJ/273K = 183J/K
b) S = 50kJ/343K = 146J/K
4.3(b)
per mole CV = 5/2R. For an ideal (perfect), gas per Cp = CV + R = 7/2R
At constant p, dqrev = dH
S = 273373[Cp/T]dT = 7/2Rn(373/273)
= 9.08J/K
4.5(b)
CV = 27.5J/K-mol q = 0 for adiabatic process
S = 0 for reversible adiabatic process
dU = CVdT = dw for the ideal gas
U = CVT = w for constant heat capacity, U = w = 2mol(27.5J/mol-K)(300K-250K)
U = w = 2.75kJ
H = U + (pV) = U + nRT = 2.75kJ + 2(8.31J/mol-K)(50K) = 3.58kJ
4.6(b)
Cp = 5/2R, T1 = 250K, T2
= 700K, V1 = 20.0L, V2=60.0L, ideal gas
GAS(T1,V1) GAS(T2, V1) GAS(T2,
V2)
For step 1, constant volume heating: dqrev = dU = CVdT
= (Cp -R)dT = 3/2R
S1 = [CV/T]dT = CVn(T2/T1)
= (3.5mol)(3/2R)n(700/250) = 44.9J/K
For step 2, isothermal expansion: dU = CVdT + TdV = 0 for ideal gas
Thus dq = -dw and for reversible expansion dqrev = +pdV =
+nRT2dV/V
Thus, dS = dqrev/T2 = nRdV/V or S = nRn(V2/V1) = 3.5mol(8.31J/mol-K)n(60.0/20.0)
S2 = 32.0J/K and S = S1 + S2 = 44.9 + 32.0 = 76.9J/K