Introduction/Background

the Bohr atom

The Bohr model provides a simplified picture of an atom, thus allowing us to study some of the most important properties of atomic and molecular structures. The Bohr model was first proposed by Niels Bohr in 1915. Although the model is not completely correct, it is sufficient for our discussion.

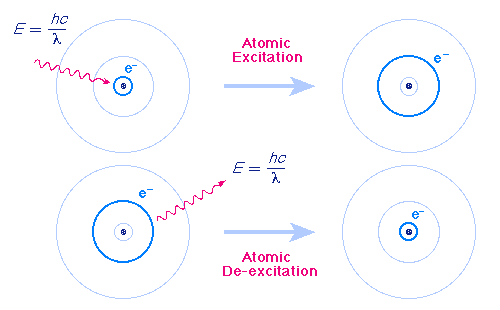Atoms can make transitions between orbits by emitting and absorbing exactly the energy difference between the orbits (See figure). This figure shows an atomic excitation caused by absorption of a photon and an atomic relaxation (de-excitation) caused by the emission of a photon. These emitted photons are what we see as color. A photon is the smallest possible amount of radiant energy, such as from light.

Key Concepts

     Quantum theory states that electrons in an atom can only have certain discrete energies. Atoms in the ground state (having a principal quantum number of n = 1) can be excited to a higher energy state (n = 5) by an external energy source such as an electrical field or flame. When these excited electrons lose energy, they emit light of quantized wavelengths and fall back down to lower energy levels (n = 4, n = 3, n = 2 or the ground state). Niels Bohr formulated an equation that would allow us to calculate the change in energy (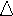E) that accompanies the leap of an electron from one energy level to another. This equation looks like:

, where n_f and n_i are energy level values.
We can rearrange this equation to solve for wavelength (Rydberg Equation).
, where is wavelength in nanometers (nm).
Finally, wavelength can be converted to frequency by the following equation:
, where c is the speed of light (3.00 x 108 ms^-1), and is frequency (s^-1).
Let's do some practice problems.

Example 1: Calculate the energy change, in joules, that occurs when an electron falls from the ni = 5 to the nf = 3 energy level in a hydrogen atom. Also calculate its wavelength and frequency at this transition. Answer:

Glossary

     
Neutron = an uncharged elementary particle that has a mass nearly equal to that of the proton and is present in all known atomic nuclei except the hydrogen nucleus.

Proton = an elementary particle that is identical with the nucleus of the hydrogen atom, that along with neutrons is a constituent of all other atomic nuclei, that carries a positive charge numerically equal to the charge of an electron, and that has a mass of 1.673 x 10¯ ²⁴ gram.

Electron = an elementary particle consisting of a charge of negative electricity equal to about 1.602 x 10 ^-19 coulomb and having a mass when at rest of about 9.109534 x 10 ^-28 gram or about 1/1836 that of a proton.

Nucleus = the positively charged central portion of an atom that comprises nearly all of the atomic mass and that consists of protons and neutrons except in hydrogen which consists of one proton only.

Radii = the plural of RADIUS, which is a line segment extending from the center of a circle or sphere to the circumference or bounding surface.

Coulombic = of, relating to, or being the electrostatic force of attraction or repulsion between charged particles.

Joule = a unit of work or energy equal to the work done by a force of one newton acting through a distance of one meter.

     

Related Materials

     Spectral Lines (http://www.colorado.edu/physics/2000/quantumzone/)
     Bunsen and Line Spectra (http://www.unit5.org/christjs/Atomic%20Structure%20Line.htm)