The MatLab script CGCA2D.m allows you to run basic examples of the two-dimensional version of our cellular automaton model capable of describing precipitate patterns in Hele-Shaw cells. The model domain consists of a regular grid of N×N cells. Each cell is occupied by either one of the reactant species (A, B) or the precipitate C. Reactant A initially occupies most of the domain while reactant B is injected during the simulation. The simple rules of the model are described in
B. C. Batista, A. Z. Morris, and O. Steinbock, "Pattern Selection by Material Aging: Modeling Chemical Gardens in Two and Three Dimensions", Proc. Natl. Acad. Sci. USA 120, e2305172120, 2023
and introduce an age bias that makes the expansion along fresh C regions more likely than in older ones.
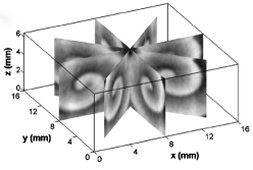

The zip file tomography.zip extracts into one MATLAB m-file and 62 jpg files. The latter images are showing different perspectives of a typical wave pattern in the Belousov-Zhabotinsky (BZ) reaction. The observation angle increases by 5.8 degrees from picture to picture. In the data provided here, the wave pattern essentially did not move (less than 5 pixels) during data aquisition.
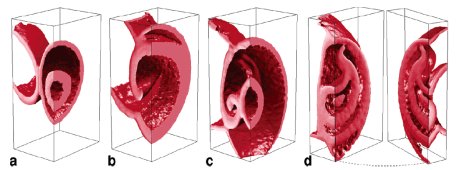
Once extracted you should change the path information in the m-file and excecute it with MATLAB. We have tested the program with MATLAB versions 6.5 and 7.4. The script requires the function IRADON from the image processing toolbox. The program will compute the three-dimensional tomographic reconstruction based on the 62 images. It will open three windows illustrating the reconstruction result in terms of (i) a reconstructed isosurface, (ii) the posterior half of it, and (iii) a slice-wise visualization. On our PCs the run time of the script is approximately 2-3 minutes.
How it Works: 3D image reconstruction is carried out slice-wise with the individual slices being normal to the rotation axis of the sample. The crucial step is to compute the inverse Radon transform of the data using "filtered backprojection". A concise description of the method is given in: Winfree et al., Chaos 6, 617-626 (1996).
About the Example: We are studying three-dimensional concentration waves in the BZ reaction. These waves are traveling zones of oxidation in a reduced medium. They are detected via local changes in the system’s absorption of white light. In simple terms, we see blue waves in a red system. During the experiment, a cylindrical cuvette with the reaction system is rotated around its symmetry axis at 12 rpm using a small electric motor and a simple belt drive. This rotation allows us to collect image data from various perspectives. Image sequences of the rotating sample are recorded with a monochrome video camera connected to PC-based frame grabber.
There is no fluid motion. The wave patterns arise from autocatalytic reactions "infecting" neighboring regions by diffusion.
The figures show data reconstructed from experiments with the BZ reaction.
The MatLab script CW.m allows you to run basic examples of a chiral walker on a square lattice. Background: The model is based on rotating walkers with trailing tails spanning L lattice bonds. These tail segments cannot overlap and their leading A segments cannot be crossed. As prescribed by their chirality, walkers must turn if possible, or go straight, or else correct earlier steps recursively. The resulting motion traces unbound trajectories and complex periodic orbits with various symmetries. Periods tend to decrease with increasing L and vary between L and L². Interacting walkers can form intricate pair states. Some orbits match pinned spiral tip trajectories observed experimentally in excitable systems. More information in: S. Dutta and O. Steinbock, "Self-avoiding Chiral Walks", Int. J. Bif. Chaos 20, 3717, 2010.